题目内容
设数列{an}的各项均为正数,它的前n项和为Sn(n∈N*),已知点(an,4Sn)在函数f (x)=x2+2x+1的图象上.(1)证明{an}是等差数列,并求an;
(2)设m、k、p∈N*,m+p=2k,求证:
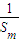 +
+ ≥
≥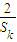 ;
;(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由.
【答案】分析:(1)由4Sn=an2+2an+1,递推得4Sn-1=an-12+2an-1+1(n≥2),两式相减整理可得(an+an-1)(an-an-1-2)=0,由an+an-1≠0,可知an-an-1=2,符合等差数列的定义.
(2)由(1)可求得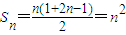 ,从而有Sm=m2,Sp=p2,Sk=k2.再作差比较.
,从而有Sm=m2,Sp=p2,Sk=k2.再作差比较.
(3)由特殊到一般可猜想结论成立,设等差数列{an}的首项为a1,公差为d,则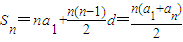 ,可证明Sm+Sp-2Sk=ma1+
,可证明Sm+Sp-2Sk=ma1+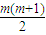 d+pa1+
d+pa1+ d-[2ka1+k(k-1)d]=(m+p)a1+
d-[2ka1+k(k-1)d]=(m+p)a1+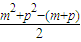 d-[2ka1+(k2-k)d]=
d-[2ka1+(k2-k)d]= •d=
•d=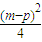 ≥0,SmSp=
≥0,SmSp=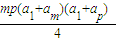 =
=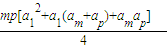 ≤
≤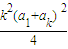 =
= ,从而得证.
,从而得证.
解答:证明:(1)∵4Sn=an2+2an+1,
∴4Sn-1=an-12+2an-1+1(n≥2).
两式相减得4an=an2-an-12+2an-2an-1.
整理得(an+an-1)(an-an-1-2)=0,
∵an+an-1≠0,
∴an-an-1=2(常数).
∴{an}是以2为公差的等差数列.又4S1=a12+2a1+1,即a12-2a1+1=0,解得a1=1,
∴an=1+(n-1)×2=2n-1.(4分)
(2)由(1)知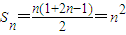 ,∴Sm=m2,Sp=p2,Sk=k2.
,∴Sm=m2,Sp=p2,Sk=k2.
由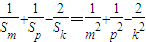 =
=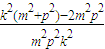
≥ ≥
≥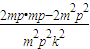 =0,
=0,
即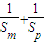 ≥
≥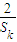 .(7分)
.(7分)
(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则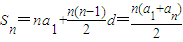 ,
,
∵Sm+Sp-2Sk=ma1+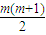 d+pa1+
d+pa1+ d-[2ka1+k(k-1)d]=(m+p)a1+
d-[2ka1+k(k-1)d]=(m+p)a1+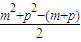 d-[2ka1+(k2-k)d],
d-[2ka1+(k2-k)d],
把m+p=2k代入上式化简得
Sm+SP-2Sk= •d=
•d=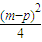 ≥0,
≥0,
∴Sm+Sp≥2Sk.
又SmSp=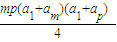 =
=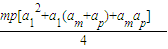
≤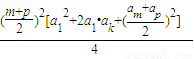
=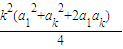
=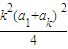 =
=
∴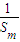 +
+ =
= ≥
≥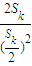 =
=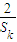 .
.
故原不等式得证.(14分)
点评:本题主要考查数列与函数,不等式的综合运用,主要涉及了等差数列通项及前n项和,不等式证明,还考查了放缩法,转化思想.
(2)由(1)可求得
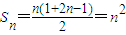 ,从而有Sm=m2,Sp=p2,Sk=k2.再作差比较.
,从而有Sm=m2,Sp=p2,Sk=k2.再作差比较.(3)由特殊到一般可猜想结论成立,设等差数列{an}的首项为a1,公差为d,则
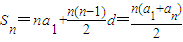 ,可证明Sm+Sp-2Sk=ma1+
,可证明Sm+Sp-2Sk=ma1+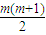 d+pa1+
d+pa1+ d-[2ka1+k(k-1)d]=(m+p)a1+
d-[2ka1+k(k-1)d]=(m+p)a1+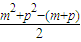 d-[2ka1+(k2-k)d]=
d-[2ka1+(k2-k)d]= •d=
•d=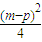 ≥0,SmSp=
≥0,SmSp=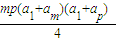 =
=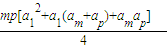 ≤
≤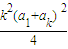 =
= ,从而得证.
,从而得证.解答:证明:(1)∵4Sn=an2+2an+1,
∴4Sn-1=an-12+2an-1+1(n≥2).
两式相减得4an=an2-an-12+2an-2an-1.
整理得(an+an-1)(an-an-1-2)=0,
∵an+an-1≠0,
∴an-an-1=2(常数).
∴{an}是以2为公差的等差数列.又4S1=a12+2a1+1,即a12-2a1+1=0,解得a1=1,
∴an=1+(n-1)×2=2n-1.(4分)
(2)由(1)知
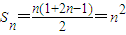 ,∴Sm=m2,Sp=p2,Sk=k2.
,∴Sm=m2,Sp=p2,Sk=k2.由
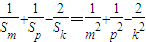 =
=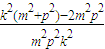
≥
 ≥
≥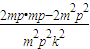 =0,
=0,即
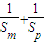 ≥
≥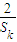 .(7分)
.(7分)(3)结论成立,证明如下:
设等差数列{an}的首项为a1,公差为d,则
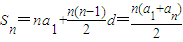 ,
,∵Sm+Sp-2Sk=ma1+
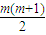 d+pa1+
d+pa1+ d-[2ka1+k(k-1)d]=(m+p)a1+
d-[2ka1+k(k-1)d]=(m+p)a1+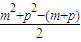 d-[2ka1+(k2-k)d],
d-[2ka1+(k2-k)d],把m+p=2k代入上式化简得
Sm+SP-2Sk=
 •d=
•d=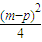 ≥0,
≥0,∴Sm+Sp≥2Sk.
又SmSp=
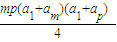 =
=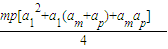
≤
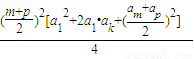
=
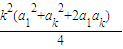
=
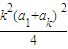 =
=
∴
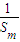 +
+ =
= ≥
≥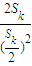 =
=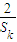 .
.故原不等式得证.(14分)
点评:本题主要考查数列与函数,不等式的综合运用,主要涉及了等差数列通项及前n项和,不等式证明,还考查了放缩法,转化思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目