题目内容
不等式|x|≤1的解集可表示为
- A.{x|x≥1}
- B.{x|x≤1}
- C.(-1,1)
- D.[-1,1]
D
分析:根据绝对值非负的特征,将不等式两边平方整理,得(x-1)(x+1)≤0,再结合一元二次不等式解法的结论,不难得到本题的答案.
解答:∵0≤|x|≤1,
∴两边平方,得x2≤1,即(x-1)(x+1)≤0
解这个不等式,得-1≤x≤1,所以原不等式的解集是[-1,1]
故选:D
点评:本题给出含有绝对值的不等式,求它的解集.着重考查了不等式等价变形、含有绝对值的不等式和一元二次不等式的解法等知识,属于基础题.
分析:根据绝对值非负的特征,将不等式两边平方整理,得(x-1)(x+1)≤0,再结合一元二次不等式解法的结论,不难得到本题的答案.
解答:∵0≤|x|≤1,
∴两边平方,得x2≤1,即(x-1)(x+1)≤0
解这个不等式,得-1≤x≤1,所以原不等式的解集是[-1,1]
故选:D
点评:本题给出含有绝对值的不等式,求它的解集.着重考查了不等式等价变形、含有绝对值的不等式和一元二次不等式的解法等知识,属于基础题.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
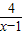 ≤x-1的解集是( )
≤x-1的解集是( )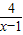 ≤x-1的解集是( )
≤x-1的解集是( )