题目内容
(5分)(2011•陕西)设集合M={y|y=|cos2x﹣sin2x|,x∈R},N={x||x﹣ |<
|< ,i为虚数单位,x∈R},则M∩N为( )
,i为虚数单位,x∈R},则M∩N为( )
| A.(0,1) | B.(0,1] | C.[0,1) | D.[0,1] |
C
解析试题分析:通过三角函数的二倍角公式化简集合M,利用三角函数的有界性求出集合M;利用复数的模的公式化简集合N;利用集合的交集的定义求出交集.
解:∵M={y|y=|cos2x﹣sin2x|}={y|y=|cos2x|}={y|0≤y≤1} ={x|﹣1<x<1}
={x|﹣1<x<1}
∴M∩N={x|0≤x<1}
故选C
点评:本题考查三角函数的二倍角公式、三角函数的有界性、复数的模的公式、集合的交集的定义.

练习册系列答案
相关题目
已知集合M={0,1,2,3}, N={x|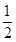 <2x<4},则集合M∩(CRN)等于( )
<2x<4},则集合M∩(CRN)等于( )
| A.{0,1,2} | B.{2,3} | C.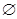 | D.{0,1,2,3} |
 的定义域为
的定义域为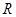 ,给定两集合
,给定两集合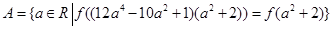 及
及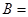
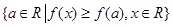 ,则集合
,则集合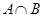 的元素个数是_________.
的元素个数是_________. ,
, ,则
,则 = .
= . ,
, ,则
,则 .
. ,
, ,则
,则 ____________.
____________.