题目内容
数列通项an=(1-2x)n(x∈R),若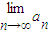 存在,则x的取值范围是( )
存在,则x的取值范围是( )A.[0,1]
B.(0,1)
C.(0,1]
D.[0,1)
【答案】分析:由数列的通项及极限的性质知,此数列的底数一定[0,1)上的数,由此关系建立不等式求出x的取值范围
解答:解:由题意数列通项an=(1-2x)n(x∈R),若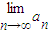 存在
存在
∴-1<1-2x≤1
解得0≤x<1
x的取值范围是[0,1)
故答案选D
点评:本题考查数列的极限,解答本题关键是正确理解极限存在这个条件,由此条件确定出数列的通项的中底数的取值范围,对题设条件的正确转化对解题很重要
解答:解:由题意数列通项an=(1-2x)n(x∈R),若
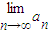 存在
存在∴-1<1-2x≤1
解得0≤x<1
x的取值范围是[0,1)
故答案选D
点评:本题考查数列的极限,解答本题关键是正确理解极限存在这个条件,由此条件确定出数列的通项的中底数的取值范围,对题设条件的正确转化对解题很重要

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列通项an=(1-2x)n(x∈R),若
an存在,则x的取值范围是( )
| lim |
| n→∞ |
| A、[0,1] |
| B、(0,1) |
| C、(0,1] |
| D、[0,1) |