题目内容
已知tanθsinθ<0,且|sinθ+cosθ|<1,则角θ是( )
分析:根据题意可求得cosθ<0,sinθ>0,从而可得答案.
解答:解:∵tanθsinθ=
•sinθ=
<0,
∴cosθ<0;
又|sinθ+cosθ|<1,
∴两边平方得:1+2sinθ•cosθ<1,
∴2sinθ•cosθ<0,而cosθ<0,
∴sinθ>0,
∴角θ是第二象限角.
故选B.
| sinθ |
| cosθ |
| sin2θ |
| cosθ |
∴cosθ<0;
又|sinθ+cosθ|<1,
∴两边平方得:1+2sinθ•cosθ<1,
∴2sinθ•cosθ<0,而cosθ<0,
∴sinθ>0,
∴角θ是第二象限角.
故选B.
点评:本题考查象限角,确定sinθ>0是关键,也是难点,考查分析转化能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 =
= tan
tan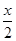 -
-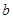 sin
sin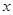 +4(其中
+4(其中
 0),如果
0),如果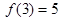 ,则
,则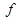 (2010
(2010 -3)的值为 ( )
-3)的值为 ( )  =sin(A+B),给出以下四个论断:
=sin(A+B),给出以下四个论断: