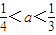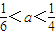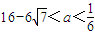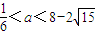题目内容
已知a、b、c是正实数，求证：| a2 |
| b2 |
| b2 |
| c2 |
| c2 |
| a2 |
| b |
| a |
| c |
| b |
| a |
| c |
分析：由实数平方的非负性可得（
-
）2+（
-
）2+（
-
）2≥0，利用不等式的性质，将其展开后，进行变形，即可证得结论．
| a |
| b |
| b |
| c |
| b |
| c |
| c |
| a |
| c |
| a |
| a |
| b |
解答：解：∵（
-
）2+（
-
）2+（
-
）2≥0
即2•（
+
+
）-2•（
+
+
）≥0
即2•（
+
+
）≥2•（
+
+
）
∴
+
+
≥
+
+
．（10分）
| a |
| b |
| b |
| c |
| b |
| c |
| c |
| a |
| c |
| a |
| a |
| b |
即2•（
| a 2 |
| b2 |
| b2 |
| c2 |
| c2 |
| a2 |
| b |
| a |
| c |
| b |
| a |
| c |
即2•（
| a 2 |
| b2 |
| b2 |
| c2 |
| c2 |
| a2 |
| b |
| a |
| c |
| b |
| a |
| c |
∴
| a 2 |
| b2 |
| b2 |
| c2 |
| c2 |
| a2 |
| b |
| a |
| c |
| b |
| a |
| c |
点评：本题考查的知识点是不等式的证明，其中分析不等式两边的形式，观察到不等号左边的平方形式，而采用平方法进行切入是解答本题的关键．
练习册系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
，关于方程
（
为正实数）的根的叙述有下列四个命题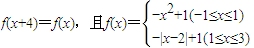 
，若方程f（x）-ax=0有5个实根，则正实数a的取值范围是（ ）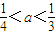
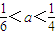
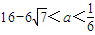
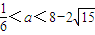
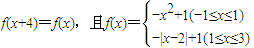，若方程f（x）-ax=0有5个实根，则正实数a的取值范围是（ ）
