题目内容
有下列四个说法:
①过三点确定一个平面;
②有三个角为直角的四边形是矩形;
③三条直线两两相交则确定一个平面;
④两个相交平面把空间分成四个区域.
其中错误说法的序号是
①过三点确定一个平面;
②有三个角为直角的四边形是矩形;
③三条直线两两相交则确定一个平面;
④两个相交平面把空间分成四个区域.
其中错误说法的序号是
①,②,③
①,②,③
.分析:由题意,①③两个命题研究的是确定一个平面的条件,由公理3及它的推论作出判断,②有三个直角的空间四边形不一定是矩形,④的判断可根据实际情况作出判断.
解答: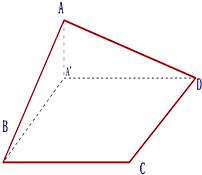 解:①由于过不共面的三点才能确定一个平面,故①不对;
解:①由于过不共面的三点才能确定一个平面,故①不对;
②如图,矩形A′BCD,A在平面A′BCD上的射影是A′,则四边形ABCD的三个角为直角,但该四边形不是矩形,故②不正确;
③由于三条直线两两相交包括三线过一点,故三条直线两两相交则确定一个平面不正确,③不对;
④两个相交平面把空间分为四个区域是正确的命题,故④正确.
综上,错误命题的序号是①,②,③.
故答案为:①,②,③.
 解:①由于过不共面的三点才能确定一个平面,故①不对;
解:①由于过不共面的三点才能确定一个平面,故①不对;②如图,矩形A′BCD,A在平面A′BCD上的射影是A′,则四边形ABCD的三个角为直角,但该四边形不是矩形,故②不正确;
③由于三条直线两两相交包括三线过一点,故三条直线两两相交则确定一个平面不正确,③不对;
④两个相交平面把空间分为四个区域是正确的命题,故④正确.
综上,错误命题的序号是①,②,③.
故答案为:①,②,③.
点评:本题考点平面的基本性质及推论,考查了公理3及其推论,及空间图形的结构,解题的关键是熟练掌握平面的基本性质及公理,从而作出判断,本题考察了空间想像能力及打理判断的能力.

练习册系列答案
相关题目