题目内容
已知函数f(x)=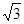 sin2x+sinxcosx-
sin2x+sinxcosx-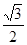 (xÎR).
(xÎR).
(1)若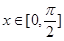 ,求f(x)的最大值;
,求f(x)的最大值;
(2)在△ABC中,若A<B,f(A)=f(B)=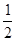 ,求
,求 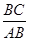 的值.
的值.
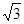 sin2x+sinxcosx-
sin2x+sinxcosx-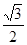 (xÎR).
(xÎR).(1)若
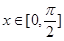 ,求f(x)的最大值;
,求f(x)的最大值;(2)在△ABC中,若A<B,f(A)=f(B)=
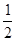 ,求
,求 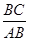 的值.
的值.(1)f(x)=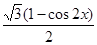 +
+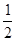 sin2x-
sin2x-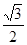 =
=
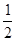 sin2x-
sin2x-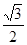 cos2x=sin(2x-
cos2x=sin(2x-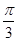 ).
).
∵0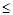 x
x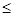
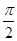 ,∴-
,∴-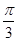
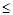 2x-
2x-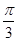
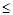
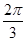 . ------------------3分
. ------------------3分
∴当2x-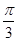 =
=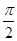 时,即x=
时,即x=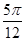 时,f(x)的最大值为1.---------------------5分
时,f(x)的最大值为1.---------------------5分
(2)∵f(x)=sin(2x-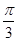 ),x是三角形的内角,则0<x<p,-
),x是三角形的内角,则0<x<p,-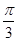 <2x-
<2x-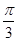 <
<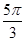
令f(x)=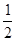 ,得sin(2x-
,得sin(2x-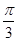 )=
)=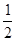 ,∴2x-
,∴2x-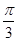 =
=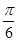 ,或2x-
,或2x-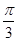 =
=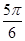 ,-------7分
,-------7分
解得x=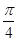 ,或x=
,或x=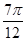 .-------------------------------------8分
.-------------------------------------8分
由已知,A,B是△ABC的内角,A<B且f(A)=f(B)=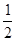 ,∴A=
,∴A=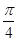 ,B=
,B=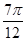 --9分
--9分
∴C=p-A-B=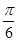 ----------------------------------------10分
----------------------------------------10分
由正弦定理,得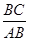 =
=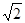 .
.
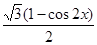 +
+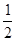 sin2x-
sin2x-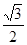 =
=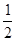 sin2x-
sin2x-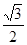 cos2x=sin(2x-
cos2x=sin(2x-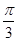 ).
).∵0
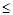 x
x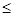
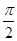 ,∴-
,∴-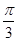
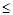 2x-
2x-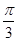
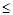
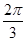 . ------------------3分
. ------------------3分∴当2x-
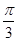 =
=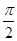 时,即x=
时,即x=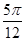 时,f(x)的最大值为1.---------------------5分
时,f(x)的最大值为1.---------------------5分(2)∵f(x)=sin(2x-
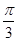 ),x是三角形的内角,则0<x<p,-
),x是三角形的内角,则0<x<p,-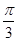 <2x-
<2x-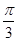 <
<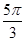
令f(x)=
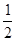 ,得sin(2x-
,得sin(2x-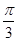 )=
)=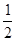 ,∴2x-
,∴2x-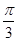 =
=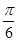 ,或2x-
,或2x-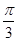 =
=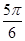 ,-------7分
,-------7分解得x=
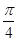 ,或x=
,或x=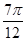 .-------------------------------------8分
.-------------------------------------8分由已知,A,B是△ABC的内角,A<B且f(A)=f(B)=
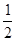 ,∴A=
,∴A=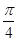 ,B=
,B=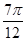 --9分
--9分∴C=p-A-B=
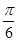 ----------------------------------------10分
----------------------------------------10分由正弦定理,得
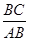 =
=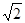 .
.略

练习册系列答案
相关题目
 中,已知
中,已知 ,且
,且

 ,则
,则 的轨迹方程()
的轨迹方程()


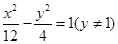
 在
在 上为增函数,其中
上为增函数,其中 ,
, 的取值集合;
的取值集合; ,若
,若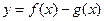 在
在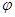 )+b(ω>0,|
)+b(ω>0,|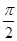 的图象的一部分如图所示。
的图象的一部分如图所示。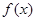 的表达式;(2)试写出
的表达式;(2)试写出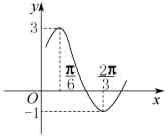
 ,其中
,其中 ,若
,若 对所有的
对所有的 恒成立,且
恒成立,且 ,则
,则 的一个单调增区间是( )
的一个单调增区间是( )
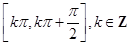


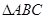 中,角A,B,C所对的边长分别为
中,角A,B,C所对的边长分别为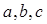 ;若
;若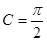 ,
,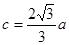 ;则
;则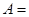 ( )
( )



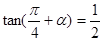 ,则
,则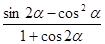 的值为
的值为



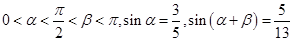 ,则
,则 .
.