题目内容
如图(1),等腰直角三角形ABC的底边AB=4,点D在线段AC上,DE⊥AB于E,现将△ADE沿DE折起到△PDE的位置(如图(2)).(Ⅰ)求证:PB⊥DE;
(Ⅱ)若PE⊥BE,直线PD与平面PBC所成的角为30°,求PE长.
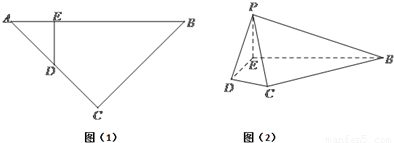
【答案】分析:(I)根据翻折后DE仍然与BE、PE垂直,结合线面垂直的判定定理可得DE⊥平面PEB,再由线面垂直的性质可得PB⊥DE;
(II)分别以DE、BE、PE所在直线为x轴、y轴、z轴,建立如图所示空间直角坐标系.设PE=a,可得点B、D、C、P关于a的坐标形式,从而得到向量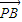 、
、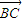 坐标,利用垂直向量数量积为0的方法建立方程组,解出平面PCD的一个法向量为
坐标,利用垂直向量数量积为0的方法建立方程组,解出平面PCD的一个法向量为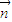 =(1,1,
=(1,1,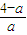 ),由PD与平面PBC所成的角为30°和向量
),由PD与平面PBC所成的角为30°和向量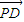 的坐标,建立关于参数a的方程,解之即可得到线段PE的长.
的坐标,建立关于参数a的方程,解之即可得到线段PE的长.
解答:解:(Ⅰ)∵DE⊥AB,∴DE⊥BE,DE⊥PE,….(2分)
∵BE∩PE=E,∴DE⊥平面PEB,
又∵PB?平面PEB,∴BP⊥DE; ….(4分)
(Ⅱ)∵PE⊥BE,PE⊥DE,DE⊥BE,
∴分别以DE、BE、PE所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),…(5分)
设PE=a,则B(0,4-a,0),D(a,0,0),C(2,2-a,0),
P(0,0,a),…(7分)
可得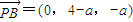 ,
,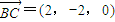 ,…(8分)
,…(8分)
设面PBC的法向量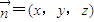 ,
,
∴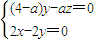 令y=1,可得x=1,z=
令y=1,可得x=1,z=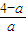
因此 是面PBC的一个法向量,…(10分)
是面PBC的一个法向量,…(10分)
∵ ,PD与平面PBC所成角为30°,…(12分)
,PD与平面PBC所成角为30°,…(12分)
∴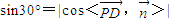 ,即
,即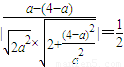 ,…(11分)
,…(11分)
解之得:a=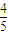 ,或a=4(舍),因此可得PE的长为
,或a=4(舍),因此可得PE的长为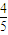 .…(13分)
.…(13分)
点评:本题给出平面图形的翻折,求证线面垂直并在已知线面角的情况下求线段PE的长,着重考查了线面垂直的判定与性质和利用空间向量研究直线与平面所成角的求法等知识,属于中档题.
(II)分别以DE、BE、PE所在直线为x轴、y轴、z轴,建立如图所示空间直角坐标系.设PE=a,可得点B、D、C、P关于a的坐标形式,从而得到向量
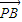 、
、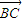 坐标,利用垂直向量数量积为0的方法建立方程组,解出平面PCD的一个法向量为
坐标,利用垂直向量数量积为0的方法建立方程组,解出平面PCD的一个法向量为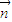 =(1,1,
=(1,1,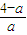 ),由PD与平面PBC所成的角为30°和向量
),由PD与平面PBC所成的角为30°和向量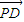 的坐标,建立关于参数a的方程,解之即可得到线段PE的长.
的坐标,建立关于参数a的方程,解之即可得到线段PE的长.解答:解:(Ⅰ)∵DE⊥AB,∴DE⊥BE,DE⊥PE,….(2分)
∵BE∩PE=E,∴DE⊥平面PEB,
又∵PB?平面PEB,∴BP⊥DE; ….(4分)
(Ⅱ)∵PE⊥BE,PE⊥DE,DE⊥BE,
∴分别以DE、BE、PE所在直线为x轴、y轴、z轴建立空间直角坐标系(如图),…(5分)

设PE=a,则B(0,4-a,0),D(a,0,0),C(2,2-a,0),
P(0,0,a),…(7分)
可得
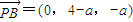 ,
,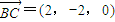 ,…(8分)
,…(8分)设面PBC的法向量
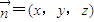 ,
,∴
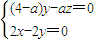 令y=1,可得x=1,z=
令y=1,可得x=1,z=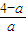
因此
 是面PBC的一个法向量,…(10分)
是面PBC的一个法向量,…(10分) ∵
 ,PD与平面PBC所成角为30°,…(12分)
,PD与平面PBC所成角为30°,…(12分)∴
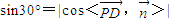 ,即
,即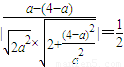 ,…(11分)
,…(11分)解之得:a=
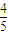 ,或a=4(舍),因此可得PE的长为
,或a=4(舍),因此可得PE的长为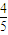 .…(13分)
.…(13分)点评:本题给出平面图形的翻折,求证线面垂直并在已知线面角的情况下求线段PE的长,着重考查了线面垂直的判定与性质和利用空间向量研究直线与平面所成角的求法等知识,属于中档题.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
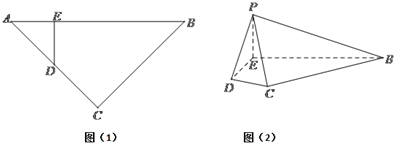
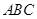 的底边
的底边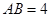 ,点
,点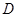 在线段
在线段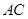 上,
上,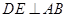 于
于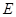 ,现将
,现将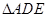 沿
沿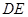 折起到
折起到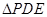 的位置(如图(2)).
的位置(如图(2)).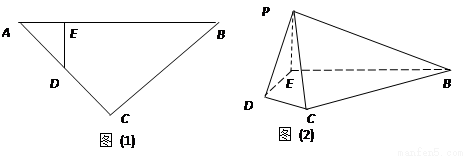
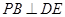 ;
;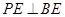 ,直线
,直线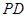 与平面
与平面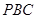 所成的角为
所成的角为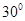 ,求
,求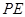 长.
长.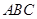 的底边
的底边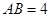 ,点
,点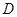 在线段
在线段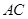 上,
上,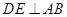 于
于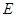 ,现将
,现将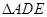 沿
沿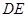 折起到
折起到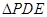 的位置(如图(2)).
的位置(如图(2)).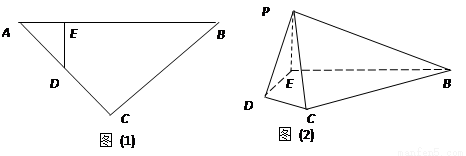
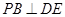 ;
;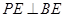 ,直线
,直线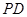 与平面
与平面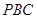 所成的角为
所成的角为 ,求
,求 长.
长. 是等腰直角三角形,其中
是等腰直角三角形,其中 ,
, 分别为
分别为 的中点,将
的中点,将 沿
沿 折起,点
折起,点 的位置变为点
的位置变为点 ,已知点
,已知点 上的射影
上的射影 为
为 的中点,如图(2)所示.
的中点,如图(2)所示.
 ;
; 的体积.
的体积.