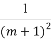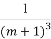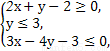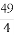题目内容
设x,y为实数,满足3≤xy2≤8,4≤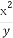 ≤9,则
≤9,则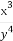 的最大值是 .
的最大值是 .
27
【解析】利用待定系数法,即令 =(
=( )m·(xy2)n,求得m,n后整体代换求解.
)m·(xy2)n,求得m,n后整体代换求解.
设 =(
=( )m(xy2)n,
)m(xy2)n,
则x3y-4=x2m+ny2n-m,
∴ 即
即
∴ =(
=( )2(xy2)-1,
)2(xy2)-1,
又由题意得( )2∈[16,81],
)2∈[16,81],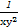 ∈[
∈[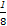 ,
, ],
],
所以 =(
=( )2
)2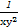 ∈[2,27],
∈[2,27],
故 的最大值是27.
的最大值是27.
【方法技巧】
1.解答本题的关键
设 =(
=( )m(xy2)n是解答本题的关键,体现了待定系数法的思想.本题是幂式之间的关系,与以往的多项式之间的关系相比较是一大创新之处,要注意这一高考新动向.
)m(xy2)n是解答本题的关键,体现了待定系数法的思想.本题是幂式之间的关系,与以往的多项式之间的关系相比较是一大创新之处,要注意这一高考新动向.
2.解决最值问题的新方法
此类问题的一般解法是先用待定系数法把目标式用己知式表示,再利用不等式的性质求出目标式的范围,对于多项式问题,也可以考虑用线性规划的方法求解.

练习册系列答案
相关题目