题目内容
(本题满分12分)一个口袋内装有大小相同的6个小球,其中2个红球,记为A1、A2,4个黑球,记为B1、B2、B3、B4,从中一次摸出2个球.
(Ⅰ)写出所有的基本事件;
(Ⅱ)求摸出的两个球颜色不同的概率.
(Ⅰ)A1,A2),(A1,B1),( A1,B2),(A1,B3),( A1,B4),(A2,B1),(A2, B2),(A2,B3),(A2,B4),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4) ;(Ⅱ)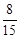 。
。
【解析】
试题分析:(Ⅰ)则从中一次摸出2个球,有如下基本事件:(A1,A2),(A1,B1),( A1,B2),(A1,B3),( A1,B4),(A2,B1),(A2, B2),(A2,B3),(A2,B4),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4) 共有15个基本事件……………….5分
(Ⅱ)从袋中的6个球中任取2个,所取的2球颜色不同的方法有:
(A1,B1),( A1,B2),(A1,B3),( A1,B4),(A2,B1),(A2, B2),(A2,B3),(A2,B4),共有8种,
故所求事件的概率P = 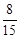 ……………………12分
……………………12分
考点:列举法计算基本事件数;随机事件发生的概率。
点评:本题考查列举法计算基本事件数及随机事件发生的概率,解题的关键是熟练运用分类列举的方法及事件的性质将所有的基本事件一一列举出来,运用公式求出概率,列举法求概率适合基本事件数不太多的概率求解问题,本题考查了分类的思想。

(本题满分12分)
一汽车厂生产A、B、C三类轿车,每类轿车有豪华型和标准型两种型号,某月生产情况如下表(单位:辆)
|
|
轿车A |
轿车B |
轿车C |
|
舒适型 |
100 |
150 |
x |
|
标准型 |
300 |
450 |
600 |
按分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(I)求x的值;
(I)列出所有基本事件,并求出至少有一辆是豪华型轿车的概率.
 吨,要装载
吨,要装载 、
、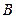 两种不同的货物,已知装载
两种不同的货物,已知装载 元,装载
元,装载 的数学期望
的数学期望 。
。 的左、右顶点分别为
的左、右顶点分别为 ,点
,点 是双曲线上不同的两个动点。
是双曲线上不同的两个动点。 与
与 交点的轨迹
交点的轨迹 的方程式;
的方程式; 与曲线
与曲线 ,已知点
,已知点 的坐标为
的坐标为 ,若点
,若点 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且 .求
.求 的值.
的值.