题目内容
.(本小题满分12分)
已知函数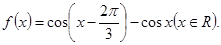
(1)求函数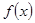 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)△ABC内角A、B、C的对边长分别为a、b、c,若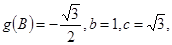
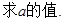
已知函数
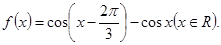
(1)求函数
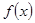 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;(2)△ABC内角A、B、C的对边长分别为a、b、c,若
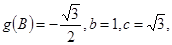
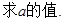
解:(1)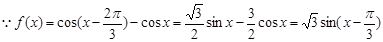 ………2分
………2分
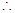 函数
函数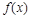 的最小正周期为
的最小正周期为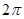 ; ………………4分
; ………………4分
递增区间为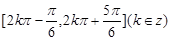
 ………………6分
………………6分
(2)
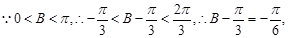 即
即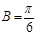 …………………9分
…………………9分
由余弦定理得: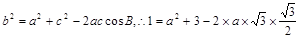 ?
?
即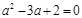 ,
, 故
故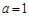 或
或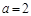 ………………12分
………………12分
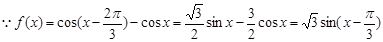 ………2分
………2分 函数
函数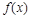 的最小正周期为
的最小正周期为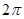 ; ………………4分
; ………………4分递增区间为
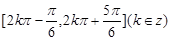
 ………………6分
………………6分(2)

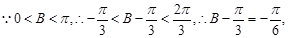 即
即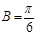 …………………9分
…………………9分由余弦定理得:
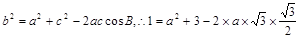 ?
?即
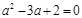 ,
, 故
故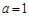 或
或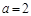 ………………12分
………………12分略

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
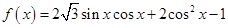
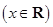 ,
,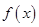 的递增区间;
的递增区间;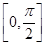 上的值域。
上的值域。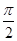 ,直线x=0是其图象的一条对称轴,求此函数的解析式.
,直线x=0是其图象的一条对称轴,求此函数的解析式.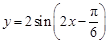 的图象( )
的图象( ) 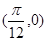 成中心对称
成中心对称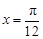 成轴对称
成轴对称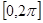 上,满足
上,满足 的
的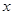 的取值范围是
的取值范围是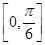
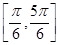
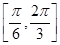
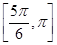
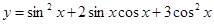 ,
,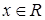 ,那么
,那么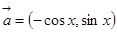 ,
,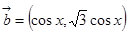 ,函数
,函数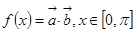 .
. 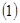 求函数
求函数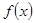 的最大值;
的最大值;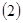 当函数
当函数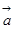 与
与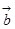 夹角的大小。
夹角的大小。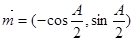 ,
, 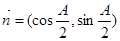 , 且
, 且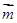 ·
·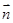 =
=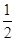 .
.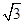 ,三角形面积S=
,三角形面积S=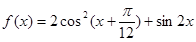
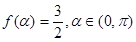 ,求
,求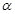 的值;
的值;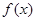 的单调增区间.
的单调增区间.