题目内容
设a,b,c都是实数.已知命题p:{a,b,c}∈{x|x⊆{a,b,c}}.命题q:若a>b>0,c≠0,则ac>bc.则下列命题中为真命题的是( )
分析:判断四个选项的真假,首先判断命题p和q的真假,对于p,因为{x|x⊆{a,b,c}}={∅,{a},{b},{c},{a,c},{a,b},{b,c},{a,b,c}},所以命题p为真命题,
对于q,若a>b>0,c<0,则ac>bc不成立,所以命题q为假命题.
对于q,若a>b>0,c<0,则ac>bc不成立,所以命题q为假命题.
解答:解:因为{x|x⊆{a,b,c}}={∅,{a},{b},{c},{a,c},{a,b},{b,c},{a,b,c}},所以命题p为真命题,
则¬p假;
若a>b>0,c<0,则ac>bc不成立,所以命题q为假命题,则¬q真.
因为¬p假,q假,所以(¬p)∨q假;
因为p真q假,所以p∧q假;
因为¬p假,¬q真,所以(¬p)∧(¬q)假;
因为p真,¬q真,所以p∧(¬q)真.
故选D.
则¬p假;
若a>b>0,c<0,则ac>bc不成立,所以命题q为假命题,则¬q真.
因为¬p假,q假,所以(¬p)∨q假;
因为p真q假,所以p∧q假;
因为¬p假,¬q真,所以(¬p)∧(¬q)假;
因为p真,¬q真,所以p∧(¬q)真.
故选D.
点评:本题考查了复合命题的真假判断,解答的关键是掌握判断复合命题真假的方法,复合命题的真值表:



练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 若
若 ,则
,则 ;命题
;命题 若
若 ,则
,则 .则下列命题中为真命题的是(
)
.则下列命题中为真命题的是(
) B.
B. C.
C. D.
D.
 若
若 ,则
,则 ;命题
;命题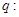 若
若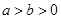 ,则
,则 .则下列命题中为真命题的是
( )
.则下列命题中为真命题的是
( ) B.
B. C.
C. D.
D.
 若
若 ,则
,则 ;命题
;命题 若
若 ,则
,则 .则下列命题中为真命题的是
( )
.则下列命题中为真命题的是
( ) B.
B. C.
C. D.
D.