题目内容
(理)椭圆
+y2=1上的点到直线x-
y+10=0的最近距离d=( )
| x2 |
| 4 |
| 3 |
分析:设椭圆
+y2=1上的点P(2cosθ,sinθ),利用点到直线间的距离公式d=
=
即可得到所求答案.
| x2 |
| 4 |
|2cosθ-
| ||
| 2 |
|
| ||
| 2 |
解答:解:∵椭圆
+y2=1的参数方程为:
,
∴设椭圆
+y2=1上的点P(2cosθ,sinθ),
则点P到直线x-
y+10=0的距离d=
=
(tanφ=-
),
∴dmin=
.
故选C.
| x2 |
| 4 |
|
∴设椭圆
| x2 |
| 4 |
则点P到直线x-
| 3 |
|2cosθ-
| ||
| 2 |
|
| ||
| 2 |
2
| ||
| 3 |
∴dmin=
10-
| ||
| 2 |
故选C.
点评:本题考查直线与圆锥曲线的关系,解决的关键在于根据椭圆的参数方程设出椭圆
+y2=1上的点P(2cosθ,sinθ),着重考查点到直线的距离公式,属于中档题.
| x2 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
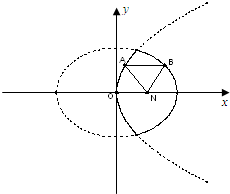 [理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆
[理]如图,已知动点A,B分别在图中抛物线y2=4x及椭圆