题目内容
已知:a≠0,f(x)=x3+ax2-a2x-1,g(x)=ax2-x-1(1)若a<0时,求y=f(x)的单调区间;
(2)若y=f(x)与y=g(x)在区间(a,a+
| 1 |
| 2 |
(3) 若y=f(x)与y=g(x)的图象有三个不同的交点,记y=g(x)在区间[0,
| 1 |
| 4 |
分析:(1)先求出导函数fˊ(x),在函数的定义域内解不等式fˊ(x)>0和fˊ(x)<0,即可求出函数的单调区间;
(2)讨论a的正负,根据函数y=f(x)与y=g(x)的单调增区间是区间(a,a+
)的子集建立方程组,解之即可;
(3)欲使y=f(x)与y=g(x)的图象有三个不同的交点,则x3+ax2-a2x-1=ax2-x-1有三个解,可求出a的范围,根据a的范围求出y=g(x)在区间[0,
]上的最小值为h(a)即可.
(2)讨论a的正负,根据函数y=f(x)与y=g(x)的单调增区间是区间(a,a+
| 1 |
| 2 |
(3)欲使y=f(x)与y=g(x)的图象有三个不同的交点,则x3+ax2-a2x-1=ax2-x-1有三个解,可求出a的范围,根据a的范围求出y=g(x)在区间[0,
| 1 |
| 4 |
解答:解:(1)f'(x)=3x2+2ax-a2=0
解得:x=
或-a
当x∈(-∞,
)或(-a,+∞)时,f'(x)>0,
则f(x)的增区间为(-∞,
),(-a,+∞)
当x∈(
,-a)时,f'(x)<0,
∴减区间为(
,-a)(4分)
(2)当a<0时,则有
得a∈(-∞,-1](7分)
当a>0时,则有
得a∈[
,+∞)(10分)
所以a∈(-∞,-1]∪[
,+∞)
(3)由x3+ax2-a2x-1=ax2-x-1得x(x2-a2+1)=0有三个解,
所以a>1或a<-1 (12分)
得h(a)=
(16分)
解得:x=
| a |
| 3 |
当x∈(-∞,
| a |
| 3 |
则f(x)的增区间为(-∞,
| a |
| 3 |
当x∈(
| a |
| 3 |
∴减区间为(
| a |
| 3 |
(2)当a<0时,则有
|
得a∈(-∞,-1](7分)
当a>0时,则有
|
得a∈[
| ||
| 2 |
所以a∈(-∞,-1]∪[
| ||
| 2 |
(3)由x3+ax2-a2x-1=ax2-x-1得x(x2-a2+1)=0有三个解,
所以a>1或a<-1 (12分)
得h(a)=
|
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,即当导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减,以及图象交点的问题,常常转化成方程根的个数,属于中档题.

练习册系列答案
相关题目
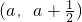 上是增函数,求a的范围;
上是增函数,求a的范围; ]上的最小值为h(a),求h(a).
]上的最小值为h(a),求h(a). 上是增函数,求a的范围;
上是增函数,求a的范围; ]上的最小值为h(a),求h(a).
]上的最小值为h(a),求h(a).