题目内容
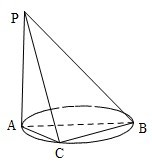 (2013•辽宁)如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(2013•辽宁)如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.(Ⅰ)求证:平面PAC⊥平面PBC;
(Ⅱ)若AB=2,AC=1,PA=1,求证:二面角C-PB-A的余弦值.
分析:(Ⅰ)要证平面PAC⊥平面PBC,只要证明平面PBC经过平面PAC的一条垂线BC即可,利用题目给出的条件借助于线面垂直的判定定理能够证明BC⊥平面PAC;
(Ⅱ)因为平面PAB和平面ABC垂直,只要在平面ABC内过C作两面的郊县AB的垂线,然后过垂足再作PB的垂线,连结C和后一个垂足即可得到二面角C-PB-A的平面角,然后在作出的直角三角形中通过解直角三角形即可求得二面角C-PB-A的余弦值.
(Ⅱ)因为平面PAB和平面ABC垂直,只要在平面ABC内过C作两面的郊县AB的垂线,然后过垂足再作PB的垂线,连结C和后一个垂足即可得到二面角C-PB-A的平面角,然后在作出的直角三角形中通过解直角三角形即可求得二面角C-PB-A的余弦值.
解答: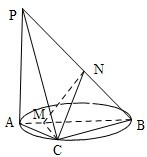 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,
由AB是圆的直径,得AC⊥BC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面APC,AC?平面PAC,
所以BC⊥平面PAC.
因为BC?平面PBC,
所以平面PAC⊥平面PBC;
(Ⅱ)解:过C作CM⊥AB于M,
因为PA⊥平面ABC,CM?平面ABC,所以PA⊥CM,
故CM⊥平面PAB.
过M作MN⊥PB于N,链接NC.
由三垂线定理得CN⊥PB.
所以∠CNM为二面角C-PB-A的平面角.
在Rt△ABC中,由AB=2,AC=1,得BC=
,CM=
,BM=
.
在Rt△ABP中,由AB=2,AP=1,得PB=
.
因为Rt△BNM∽Rt△BAP,所以
=
.
故MN=
.
又在Rt△CNM中,CN=
.故cos∠CNM=
.
所以二面角C-PB-A的余弦值为
.
 (Ⅰ)证明:如图,
(Ⅰ)证明:如图,由AB是圆的直径,得AC⊥BC.
由PA⊥平面ABC,BC?平面ABC,得PA⊥BC.
又PA∩AC=A,PA?平面APC,AC?平面PAC,
所以BC⊥平面PAC.
因为BC?平面PBC,
所以平面PAC⊥平面PBC;
(Ⅱ)解:过C作CM⊥AB于M,
因为PA⊥平面ABC,CM?平面ABC,所以PA⊥CM,
故CM⊥平面PAB.
过M作MN⊥PB于N,链接NC.
由三垂线定理得CN⊥PB.
所以∠CNM为二面角C-PB-A的平面角.
在Rt△ABC中,由AB=2,AC=1,得BC=
| 3 |
| ||
| 2 |
| 3 |
| 2 |
在Rt△ABP中,由AB=2,AP=1,得PB=
| 5 |
因为Rt△BNM∽Rt△BAP,所以
| MN |
| 1 |
| ||
|
故MN=
3
| ||
| 10 |
又在Rt△CNM中,CN=
| ||
| 5 |
| ||
| 4 |
所以二面角C-PB-A的余弦值为
| ||
| 4 |
点评:本题考查了平面与平面垂直的判定,考查了二面角的平面角及其求法,“寻找垂面,构造垂线”是找二面角的平面角常用的方法,此题是中档题.

练习册系列答案
相关题目
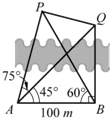 (2013•辽宁二模)风景秀美的凤凰湖畔有四棵高大的银杏树,记做A、B、P、Q,欲测量P、Q两棵树和A、P两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得A、B两点间的距离为AB=100米,如图,同时也能测量出∠PAB=75°,∠QAB=45°,∠PBA=60°,∠QBA=90°,则P、Q两棵树和A、P两棵树之间的距离各为多少?
(2013•辽宁二模)风景秀美的凤凰湖畔有四棵高大的银杏树,记做A、B、P、Q,欲测量P、Q两棵树和A、P两棵树之间的距离,但湖岸部分地方围有铁丝网不能靠近,现在可以方便的测得A、B两点间的距离为AB=100米,如图,同时也能测量出∠PAB=75°,∠QAB=45°,∠PBA=60°,∠QBA=90°,则P、Q两棵树和A、P两棵树之间的距离各为多少? (2013•辽宁一模)如图,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有( )
(2013•辽宁一模)如图,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有( )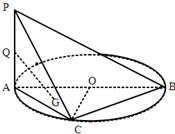 (2013•辽宁)如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆O上的点.
(2013•辽宁)如图,AB是圆O的直径,PA⊥圆O所在的平面,C是圆O上的点.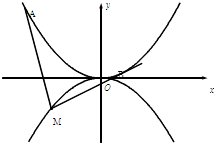 (2013•辽宁)如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1-
(2013•辽宁)如图,抛物线C1:x2=4y,C2:x2=-2py(p>0),点M(x0,y0)在抛物线C2上,过M作C1的切线,切点为A,B(M为原点O时,A,B重合于O),当x0=1-