Question

设集合是函数的定义域，集合是函数的值域.

（Ⅰ）求集合;

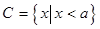（Ⅱ）设集合，若集合，求实数的取值范围.

 

Answer 1

【答案】

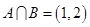(Ⅰ);(Ⅱ).

【解析】

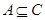试题分析：(Ⅰ)因为集合是函数的定义域,得,解得,即集合,又因为集合是函数的值域,而,得,即集合,故所求集合.(Ⅱ)由(Ⅰ)知,由,所以,即有,从而可得所求实数的取值范围为.

试题解析：(Ⅰ)由题意得,解得,即集合

因为,所以,即集合

故所求集合.

(Ⅱ)由(Ⅰ)知,又,所以,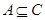

即有,

从而可得所求实数的取值范围为.

考点：1.函数的定义域、值域;2.集合的运算.