题目内容
某化工厂打算投入一条新的生产线,但需要经环保部门审批同意方可投入生产,已知该厂连续生产n个月的累计产量为f(n)=| 1 |
| 2 |
(1)请你代表环保部门给厂拟定最长的生产周期;
(2)若该厂在环保部门的规定下生产,但需要每月交纳a万元的环保税,已知每吨产品售价0.6万元,第n个月的工人工资为g(n)=
| 8 |
| 5 |
| 2 |
| 5 |
分析:(1)先化简得到第n个月的产量函数,再令f(n)-f(n-1)≤96,解得:-
≤n≤6;
(2)建立利润函数F(n)=
(3n2-2n)-a-g(n),n∈N,n≤6,则F(n)>0恒成立,求得a的范围.
| 16 |
| 3 |
(2)建立利润函数F(n)=
| 3 |
| 5 |
解答:解:(1)第n个月的月产量=
.(3分)
∵f(n)=
n(n+1)(2n-1),∴f(1)=1,当n≥2时,f(n-1)=
(n-1)n(2n-3),
∴f(n)-f(n-1)=3n2-2n.(6分)
令f(n)-f(n-1)≤96,即3n2-2n-96≤0,解得:-
≤n≤6,
∵n∈N,∴nmax=6.(9分)
(2)若每月都赢利,
则
(3n2-2n)-a-g(n)>0,n∈N,n≤6恒成立.
即a<
(n-2)2+
,n=1,2,3,4,5,6,恒成立,(12分)
令h(n)=
(n-2)2+
,n=1,2,3,4,5,6,∴n=2时h(n)最小,且h(2)=
(14分)
所以0<a<
.(16分)
|
∵f(n)=
| 1 |
| 2 |
| 1 |
| 2 |
∴f(n)-f(n-1)=3n2-2n.(6分)
令f(n)-f(n-1)≤96,即3n2-2n-96≤0,解得:-
| 16 |
| 3 |
∵n∈N,∴nmax=6.(9分)
(2)若每月都赢利,
则
| 3 |
| 5 |
即a<
| 1 |
| 5 |
| 1 |
| 5 |
令h(n)=
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
所以0<a<
| 1 |
| 5 |
点评:本题主要考查函数的实际应用,建模和解模的能力.

练习册系列答案
相关题目
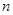 年的累计产量为
年的累计产量为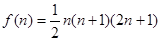 吨,但如果年产量超过
吨,但如果年产量超过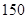 吨,会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是
吨,会给环境造成危害.为保护环境,环保部门应给该厂这条生产线拟定最长的生产期限是