题目内容
三边长分别为1,1,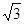 的三角形的最大内角的度数是
的三角形的最大内角的度数是
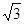 的三角形的最大内角的度数是
的三角形的最大内角的度数是A.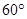 | B.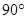 | C. | D.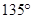 |
C
分析:设出最大内角,由三角形的三边长,利用余弦定理求出最大角的余弦函数值,由最大角的范围,利用特殊角的三角函数值即可求出最大内角的度数.
解答:解:设最大内角为α,
根据余弦定理得:(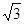 )2=1+1-2cosα,
)2=1+1-2cosα,
即cosα=-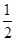 ,又α∈(0,180°),
,又α∈(0,180°),
则最大内角的度数是120°.
故选C
解答:解:设最大内角为α,
根据余弦定理得:(
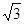 )2=1+1-2cosα,
)2=1+1-2cosα,即cosα=-
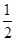 ,又α∈(0,180°),
,又α∈(0,180°),则最大内角的度数是120°.
故选C

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,
中, ,则
,则 ( )
( )



 ABC中,
ABC中, 则使
则使 的范围是( )
的范围是( )



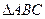 中角
中角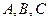 所对的边长分别为
所对的边长分别为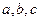 ,且
,且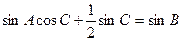 .
.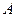 的大小; (Ⅱ)若
的大小; (Ⅱ)若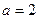 ,求
,求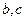 值.
值.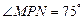 ,
,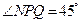 ,
,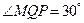 ,
,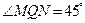 ,试求两个目标物M,N之间的距离.
,试求两个目标物M,N之间的距离.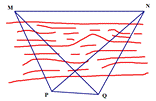
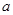 、
、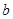 、
、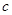 ,若
,若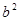 =
=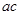 ,且
,且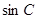 =2
=2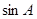 ,则
,则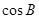 等于( )
等于( )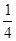 B、
B、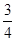 C、
C、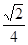 D、
D、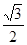
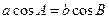 ,则这个三角形的形状是 三角形
,则这个三角形的形状是 三角形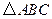 中,
中,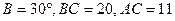 ,则
,则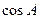 的值是______.
的值是______. 中,角
中,角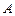 ,
,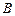 ,
,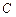 的对边的边长分别为
的对边的边长分别为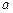 ,
,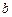 ,
,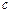 ,且
,且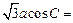
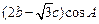 .
.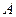 的大小;
的大小;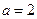 ;②
;②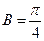 ;③
;③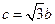 .
. 的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)
的面积.(只需写出一个选定方案即可,选多种方案以第一种方案记分)