题目内容
已知椭圆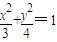 的焦点F与抛物线C:y2=2px(p>0)的焦点关于直线x-y=0对称.
的焦点F与抛物线C:y2=2px(p>0)的焦点关于直线x-y=0对称.(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab≠0,b2≠4a),M是抛物线C上的点,设直线AM,BM与抛物线的另一交点为M1,M2.求证:当M点在抛物线上变动时(只要M1,M2存在且M1≠M2)直线M1M2恒过一定点,并求出这个定点的坐标.
【答案】分析:(Ⅰ)根据题意可知椭圆的a,b,求得c进而求得椭圆的焦点,利用点关于直线的对称求得抛物线的焦点,求得p,则抛物线的方程可得.
(Ⅱ)设M,M1,M2的坐标由三点共线,利用斜率相等整理求得y1与y的关系,同样的道理可求得y2与y的关系,设(x,y)是直线M1,M2上的任意一点,求得y1y2=y(y1+y2)-4x把y1y2代入整理,利用等式恒成立建立方程组求得x和y,进而可判断出动直线M1,M2恒过定点.
解答:解:(Ⅰ)∵a=2,b=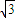 ,∴c=1
,∴c=1
椭圆的焦点在y轴上,即F(0,1),F关于直线x-y=0对称的点为(1,0);
而抛物线的焦点坐标为(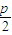 ,0)p=2,所以所求抛物线的方程为y2=4x
,0)p=2,所以所求抛物线的方程为y2=4x
(Ⅱ)证明:设M,M1,M2的坐标分别为
由A、M、M1三点共线得: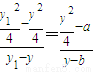 ,
,
化简得y1y=b(y1+y)-4a,
∴y1= ;
;
同理,由B、M、M2三点共线得:y2=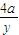
设(x,y)是直线M1,M2上的任意一点,则y1y2=y(y1+y2)-4x;
把y1y2代入上式整理得:y2(4x-by)+4by(a-x)+4a(by-4a)=0;
由M是任意的,则有 ,
,
所以动直线M1,M2恒过定点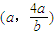
点评:圆锥曲线和直线是解析几何的主线,考查学生的运算能力是解析几何的重要部分,特别是包含比较多字母的运算,同时也考查了“设而不求”的解题策略和数形结合的数学思想方法.
(Ⅱ)设M,M1,M2的坐标由三点共线,利用斜率相等整理求得y1与y的关系,同样的道理可求得y2与y的关系,设(x,y)是直线M1,M2上的任意一点,求得y1y2=y(y1+y2)-4x把y1y2代入整理,利用等式恒成立建立方程组求得x和y,进而可判断出动直线M1,M2恒过定点.
解答:解:(Ⅰ)∵a=2,b=
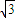 ,∴c=1
,∴c=1椭圆的焦点在y轴上,即F(0,1),F关于直线x-y=0对称的点为(1,0);
而抛物线的焦点坐标为(
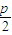 ,0)p=2,所以所求抛物线的方程为y2=4x
,0)p=2,所以所求抛物线的方程为y2=4x(Ⅱ)证明:设M,M1,M2的坐标分别为

由A、M、M1三点共线得:
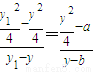 ,
,化简得y1y=b(y1+y)-4a,
∴y1=
 ;
;同理,由B、M、M2三点共线得:y2=
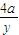
设(x,y)是直线M1,M2上的任意一点,则y1y2=y(y1+y2)-4x;
把y1y2代入上式整理得:y2(4x-by)+4by(a-x)+4a(by-4a)=0;
由M是任意的,则有
 ,
,所以动直线M1,M2恒过定点
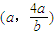
点评:圆锥曲线和直线是解析几何的主线,考查学生的运算能力是解析几何的重要部分,特别是包含比较多字母的运算,同时也考查了“设而不求”的解题策略和数形结合的数学思想方法.

练习册系列答案
相关题目
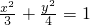 的焦点F与抛物线C:y2=2px(p>0)的焦点关于直线x-y=0对称.
的焦点F与抛物线C:y2=2px(p>0)的焦点关于直线x-y=0对称. 的焦点为
的焦点为 ,抛物线
,抛物线 与椭圆在第一象限的交点为
与椭圆在第一象限的交点为 ,若
,若 。
。 的面积;
的面积;
 的焦点F与抛物线C:
的焦点F与抛物线C: 的焦点关于直线x-y=0
的焦点关于直线x-y=0 ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM, .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要 )直线
)直线 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.