题目内容
设抛物线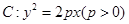 的焦点为
的焦点为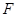 ,经过点
,经过点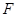 的动直线
的动直线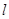 交抛物线
交抛物线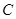 于点
于点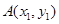 ,
,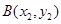 且
且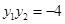 .
.
(1)求抛物线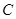 的方程;
的方程;
(2)若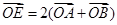 (
(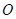 为坐标原点),且点
为坐标原点),且点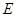 在抛物线
在抛物线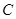 上,求直线
上,求直线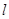 倾斜角;
倾斜角;
(3)若点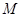 是抛物线
是抛物线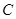 的准线上的一点,直线
的准线上的一点,直线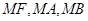 的斜率分别为
的斜率分别为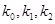 .求证:
.求证:
当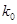 为定值时,
为定值时,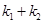 也为定值.
也为定值.
【答案】
(1)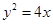 (2)倾斜角为
(2)倾斜角为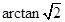 或
或 (3)
(3)
【解析】
试题分析:⑴根据题意可知: ,设直线
,设直线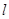 的方程为:
的方程为: ,则:
,则:
联立方程: ,消去
,消去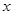 可得:
可得: (*),
(*),
根据韦达定理可得: ,∴
,∴ ,∴
,∴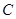 :
: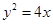
⑵设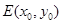 ,则:
,则: ,由(*)式可得:
,由(*)式可得:
∴ ,
,
又 ,∴
,∴
∴
∵ ,∴
,∴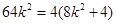 ,∴
,∴ ,∴
,∴
∴直线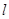 的斜率
的斜率 ,∴倾斜角为
,∴倾斜角为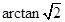 或
或
⑶可以验证该定值为 ,证明如下:
,证明如下:
设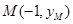 ,则:
,则: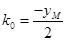 ,
, ,
,
∵ ,∴
,∴
∴


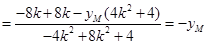
∴ 为定值
为定值
考点:抛物线
点评:考查了直线与抛物线的位置关系的运用,体现了运用代数的方法求解解析几何的运用,属于基础题。

练习册系列答案
相关题目
 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为 ,在抛物线上任意画一个点
,在抛物线上任意画一个点 ,度量点
,度量点 ,如图.
,如图.
 时,
时, ,试求抛物线
,试求抛物线 的方程;
的方程; ,焦点为
,焦点为 ,构造直线
,构造直线 交抛物线
交抛物线 ,构造直线
,构造直线 、
、 分别交准线于
分别交准线于 、
、 两点,构造直线
两点,构造直线 、
、 .经观察得:沿着抛物线
.经观察得:沿着抛物线 .请你证明这一结论.
.请你证明这一结论. 
 ”,其余条件不变,发现“
”,其余条件不变,发现“
