题目内容
已知集合A= ,集合B={(x,y)|x2+(y-a)2≤1}, 若A∩B=B,则a的取值范围是( )
,集合B={(x,y)|x2+(y-a)2≤1}, 若A∩B=B,则a的取值范围是( )
| A.[2,+∞) | B.(-∞,-2] |
| C.[-2,2] | D.(-∞,-2]∪[2,+∞) |
B
解析试题分析:因为分析题意可知, 集合A表示的为直线的一侧的区域,而集合B表示的为圆心为(0,a),半径为1的圆的内部,包括圆周,那么要使得A∩B=B,则说明B是A的子集,那么可知圆心到直线的距离大于等于圆的半径即可。可知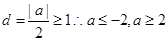 (舍),同时要注意,圆心在x轴的下方,那么可知选B.
(舍),同时要注意,圆心在x轴的下方,那么可知选B.
考点:本试题考查了集合的交集运算,以及不等式的求解。
点评:解决该试题的关键是理解集合A,B表示的含义,利用直线与圆的几何意义,分析满足A∩B=B,的集合B,得到参数a的范围。属于中档题。

练习册系列答案
相关题目
设全集U=R,集合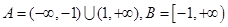 ,则下列关系正确的是( )
,则下列关系正确的是( )
A.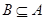 | B.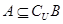 | C.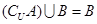 | D.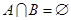 |
已知全集 ,
,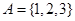 ,
,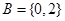 ,则
,则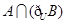 等于
等于
A.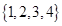 | B.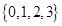 | C.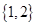 | D.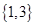 |
已知集合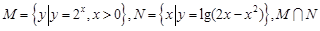 为
为
A.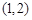 | B. | C.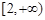 | D.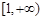 |
已知集合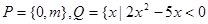 ,
,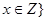 ,若
,若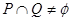 ,则
,则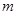 等于( )
等于( )
| A.1 | B.1或2 | C.1或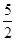 | D.2 |
设集合 ,
, ,则
,则 等于( )
等于( )
A. | B. |
C. | D.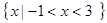 |
若集合 ,那么
,那么 ( )
( )
A. | B. | C. | D.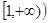 |
设集合A = {1,2,3},集合B =" {1,2,4,5}," 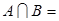 ( )
( )
| A.{1,2,3,4,5} | B.{1,2} | C.{1,2,3} | D.{4,5} |
已知集合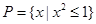 ,
,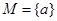 ,若
,若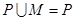 ,则a的取值范围是( )
,则a的取值范围是( )
A.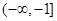 | B.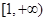 | C.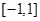 | D.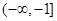 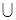 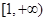 |