题目内容
已知函数 .
.
(I)
当 ,求
,求 的最小值;
的最小值;
(II)
若函数 在区间
在区间 上为增函数,求实数
上为增函数,求实数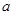 的取值范围;
的取值范围;
(III)过点 恰好能作函数
恰好能作函数 图象的两条切线,并且两切线的倾斜角互补,求实数
图象的两条切线,并且两切线的倾斜角互补,求实数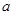 的取值范围.
的取值范围.
【答案】
(I)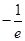 ;(II)
;(II) ;(III)
;(III) .
.
【解析】
试题分析:(I)先解得函数 的定义域,再利用导数判断函数的单调性,并求最小值;(II)先对函数
的定义域,再利用导数判断函数的单调性,并求最小值;(II)先对函数 求导,由
求导,由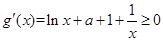 ,再分离变量
,再分离变量 得
得 ,构造新函数
,构造新函数 ,再利用导数求
,再利用导数求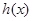 在区间
在区间 上的最小值
上的最小值 ,由
,由 可求得
可求得 的取值范围;(III),设两切点A、B坐标,利用导数求过点
的取值范围;(III),设两切点A、B坐标,利用导数求过点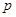 的两切线斜率,即可得方程,由条件列方程组求M、N两点的横坐标关系,根据判别式大于0可解得
的两切线斜率,即可得方程,由条件列方程组求M、N两点的横坐标关系,根据判别式大于0可解得 的取值范围.
的取值范围.
试题解析:(I)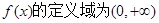 ,
, 1分
1分
 的变化的情况如下:
的变化的情况如下:
|
|
|
|
|
|
|
— |
0 |
+ |
|
|
|
极小值 |
|
3分
所以, 4分
4分
(II)
由题意得: 5分
5分
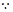 函数
函数 在区间
在区间 上为增函数,
上为增函数,
 当
当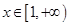 时
时 ,即
,即 在
在 上恒成立,
上恒成立,
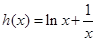 ,
7分
,
7分
 ,
,
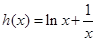 在
在 上递增
上递增
 ,
,
 10分
10分
(III)设两切点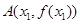 ,
, ,
,

则函数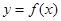 在
在 处的切线方程分别为
处的切线方程分别为
 ,
,
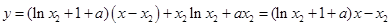
且
即 也即
也即
即 是方程
是方程 的两个正根
的两个正根
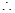

 15分
15分
考点:1、利用导数判断函数的单调性与极值;2、分离变量法.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目


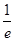





 .
.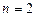 时,若函数
时,若函数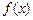 在
在 上单调递减,求实数
上单调递减,求实数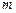 的取值范围;
的取值范围;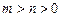 ,
, ,且过原点存在两条互相垂直的直线与曲线
,且过原点存在两条互相垂直的直线与曲线 的值.
的值. .
.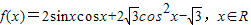 .
. ,,求△ABC的面积.
,,求△ABC的面积. ,且
,且 .(I)求
.(I)求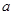 的值;(II)求函数
的值;(II)求函数 在[1,3]上的最小值和最大值.
在[1,3]上的最小值和最大值.