题目内容
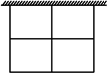
 如图,动物园要围成相同的长方形(无盖)虎笼四间,一面可以用原有的墙,其他各面用钢丝网围成.
如图,动物园要围成相同的长方形(无盖)虎笼四间,一面可以用原有的墙,其他各面用钢丝网围成.
(1)若使每间虎笼面积为24m2,则每间虎笼的长和宽各设计为多少时,可使围成四间虎笼的钢丝网总长度最小?
(2)若现有36m长钢丝网,则每间虎笼的长和宽各设计为多少时,可使每间虎笼的面积最大?
解:(1)设每间虎笼长为x米,宽为 y米,每间虎笼的面积为S,则由条件知S=xy=24.
设钢筋网总长为l,则l=4x+5y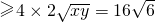
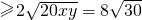
当且仅当4x=5y,即x= ,y=
,y=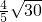 时等号成立.
时等号成立.
故每间虎笼长 m,宽
m,宽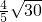 m,可使钢筋网总长最小.
m,可使钢筋网总长最小.
(2)设每间虎笼长为x米,宽为 y米,则由条件知4x+5y=36,设每间虎笼的面积为S,则S=xy.
根据4x+5y=36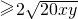 ,∴
,∴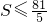 ,当且仅当4x=5y,即x=
,当且仅当4x=5y,即x= ,y=
,y= 时等号成立.
时等号成立.
故每间虎笼长为4.5 m,宽为3.6 m时,可使面积最大.
分析:(1)设每间虎笼长为x米,宽为 y米,每间虎笼的面积为S,则由条件知S=xy=24,利用基本不等式求4x+5y的最小值.
(2)设每间虎笼长为x米,宽为 y米,则由条件知4x+5y=36,设每间虎笼的面积为S,则利用基本不等式求S=xy的最大值.
点评:本题以实际问题为载体,考查基本不等式的运用,解题的关键是寻求每间虎笼长与宽的关系,进而利用基本不等式.
设钢筋网总长为l,则l=4x+5y
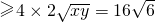
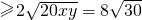
当且仅当4x=5y,即x=
 ,y=
,y=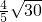 时等号成立.
时等号成立.故每间虎笼长
 m,宽
m,宽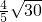 m,可使钢筋网总长最小.
m,可使钢筋网总长最小.(2)设每间虎笼长为x米,宽为 y米,则由条件知4x+5y=36,设每间虎笼的面积为S,则S=xy.
根据4x+5y=36
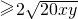 ,∴
,∴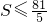 ,当且仅当4x=5y,即x=
,当且仅当4x=5y,即x= ,y=
,y= 时等号成立.
时等号成立.故每间虎笼长为4.5 m,宽为3.6 m时,可使面积最大.
分析:(1)设每间虎笼长为x米,宽为 y米,每间虎笼的面积为S,则由条件知S=xy=24,利用基本不等式求4x+5y的最小值.
(2)设每间虎笼长为x米,宽为 y米,则由条件知4x+5y=36,设每间虎笼的面积为S,则利用基本不等式求S=xy的最大值.
点评:本题以实际问题为载体,考查基本不等式的运用,解题的关键是寻求每间虎笼长与宽的关系,进而利用基本不等式.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 如图,动物园要围成相同的长方形(无盖)虎笼四间,一面可以用原有的墙,其他各面用钢丝网围成.
如图,动物园要围成相同的长方形(无盖)虎笼四间,一面可以用原有的墙,其他各面用钢丝网围成.