题目内容
记关于x的不等式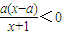
的解集为P，不等式|x-1|≤1的解集为Q．（1）若a=3，求P；
（2）若a＞-1且Q⊆P，求a的取值范围．
【答案】分析：（1）分式不等式 
的解法，可转化为整式不等式（x-a）（x+1）＜0来解；
（2）对于（II）中条件Q⊆P，应结合数轴来解决．
解答：
解：（1）若a=3，由 
，得P={x|-1＜x＜3}．
（2）Q={x||x-1|≤1}={x|0≤x≤2}．
当a＞0，得P={x|-1＜x＜a}，又Q⊆P，结合图形
所以a＞2，即a的取值范围是（2，+∞）．
当-1＜a＜0时，
?-a（x-a）（x+1）＞0，P=（-∞，-1）∪（a，+∞），这时有Q⊆P．
综上所述，a的取值范围是：（-1，0）∪（2，+∞）
点评：对于条件Q⊆P的问题，应结合数轴来解决，这样来得直观清楚，便于理解．
的解法，可转化为整式不等式（x-a）（x+1）＜0来解；（2）对于（II）中条件Q⊆P，应结合数轴来解决．
解答：
解：（1）若a=3，由 ，得P={x|-1＜x＜3}．（2）Q={x||x-1|≤1}={x|0≤x≤2}．
当a＞0，得P={x|-1＜x＜a}，又Q⊆P，结合图形
所以a＞2，即a的取值范围是（2，+∞）．
当-1＜a＜0时，
?-a（x-a）（x+1）＞0，P=（-∞，-1）∪（a，+∞），这时有Q⊆P．综上所述，a的取值范围是：（-1，0）∪（2，+∞）
点评：对于条件Q⊆P的问题，应结合数轴来解决，这样来得直观清楚，便于理解．
练习册系列答案
相关题目
等式
的解集为P， 不等式（x-1）2 ≤1的解集为Q． 
，求P；
P，求正数a的取值范围．
的解集为P，不等式
的解集为Q.
求正数a的取值范围
的解集为P， 不等式（x-1）2 ≤1的解集为Q． 
，求P；
P，求正数a的取值范围．
的解集为P，不等式|x-1|≤1的解集为Q．
的解集为P，不等式|x-1|≤3的解集为Q．