题目内容
15.在△ABC中,角A、B、C的对边分别是a、b、c,则下列各式正确的是( )| A. | $\frac{a}{sinB}=\frac{b}{sinA}$ | B. | $\frac{a}{cosA}=\frac{b}{cosB}$ | C. | asinB=bsinA | D. | asinC=csinB |
分析 △ABC中,由正弦定理可得 $\frac{a}{sinA}=\frac{b}{sinB}$,变形可得结论.
解答 解:在△ABC中,由正弦定理可得 $\frac{a}{sinA}=\frac{b}{sinB}$,即 asinB=bsinA,
故选:C.
点评 本题主要考查正弦定理的应用,属于基础题.

练习册系列答案
 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
10.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x-y+2≤0}\\{x≥1}\\{x+y-7≤0}\end{array}\right.$,则$\frac{y+x}{x}$的取值范围是( )
| A. | [$\frac{14}{5}$,7] | B. | (-∞,$\frac{14}{5}$]∪[7,+∞) | C. | (-∞,4]∪[7,+∞) | D. | (4,7] |
7.设f(x)是定义在R上的函数,若对任意的实数x,都有f(x+4)≤f(x)+4和f(x+2)≥f(x)+2且f(-1)=0,则f(2015)的值是( )
| A. | 2014 | B. | 2015 | C. | 2016 | D. | 2017 |
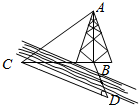 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.
如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个观测点C与D,测得∠BCD=15°,∠BDC=30°,CD=30m,并在C测得塔顶A的仰角为60°,则塔的高度为15$\sqrt{6}$m.