题目内容
已知函数![]() 满足
满足![]() ,且
,且![]()
(1)当![]() 时,求
时,求![]() 的表达式;
的表达式;
(2)设![]() ,
,![]() ,求证:
,求证:![]() ;w.w.w.k.s.5.u.c.o.m
;w.w.w.k.s.5.u.c.o.m ![]()
(3)设![]() ,对每一个
,对每一个![]() ,在
,在![]() 与
与![]() 之间插入
之间插入![]() 个
个![]() ,得到新数列
,得到新数列![]() ,设
,设![]() 是数列
是数列![]() 的前
的前![]() 项和,试问是否存在正整数
项和,试问是否存在正整数![]() ,使
,使![]() ?若存在求出
?若存在求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解析:(1)令![]() 得,
得,![]() ,………………2分
,………………2分
![]() ,公比为q=
,公比为q=![]() 的等比数列,得
的等比数列,得![]() ………………4分
………………4分
(2)证明:![]() ,
,
由错位相减法得![]() ………………8分
………………8分
(3)![]() …………………9分
…………………9分
∴在数列![]() 中,
中,![]() 及其前面所有项之和为
及其前面所有项之和为
![]() …11分
…11分
![]() ,即
,即![]()
12分
又![]() 在数列
在数列![]() 中的项数为:
中的项数为:![]() …… …… 13分
…… …… 13分
且![]() ,
,

练习册系列答案
相关题目


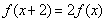

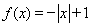

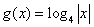
 满足
满足 ,且
,且 在区间
在区间 和区间
和区间 上分别单调。
上分别单调。 求
求 的值。
的值。 满足
满足 ,且当
,且当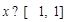 时,
时,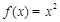 ,则
,则 与
与 的图象的交点个数为( )
的图象的交点个数为( )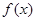 满足
满足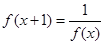 ,且
,且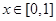 时,
时,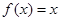 ,若在区间
,若在区间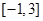 内,函数
内,函数 有4个零点,则实数
有4个零点,则实数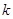 的取值范围是 .
的取值范围是 .
 满足
满足 ,且
,且 的导函数
的导函数 ,则
,则 的解集为( )
的解集为( )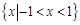 B.
B. C.
C. D.
D.