题目内容
(理)设双曲线C:
-
=1(a>0,b>0)的离心率为e,若准线l与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.
(1)求双曲线C的离心率e的值;
(2)若双曲线C被直线y=ax+b截得的弦长为
求双曲线c的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求双曲线C的离心率e的值;
(2)若双曲线C被直线y=ax+b截得的弦长为
| b2e2 |
| a |
分析:(1)根据双曲线方程可知,双曲线C的右准线l的方程为:x=
,两条渐近线方程为:y=±
x,从而可得两交点坐标,根据△PFQ为等边三角形,则有|MF|=
|PQ|,从而可建立方程c-
=
•(
+
),利用c2-a2=b2,即可求得双曲线C的离心率e的值;
(2)由(1)得双曲线C的方程为
-
=1.把y=ax+
a代入得(a2-3)x2+2
a2x+6a2=0.
利用韦达定理及弦长公式l=
,可求弦长,利用双曲线C被直线y=ax+b截得的弦长为
,建立方程,可求a2的值,从而得到双曲线C的方程.
| a2 |
| c |
| b |
| a |
| ||
| 2 |
| a2 |
| c |
| ||
| 2 |
| ab |
| c |
| ab |
| c |
(2)由(1)得双曲线C的方程为
| x2 |
| a2 |
| y2 |
| 3a2 |
| 3 |
| 3 |
利用韦达定理及弦长公式l=
| (x1-x2)2+(y1-y2)2 |
| b2e2 |
| a |
解答: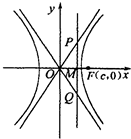 解:(1)双曲线C的右准线l的方程为:x=
解:(1)双曲线C的右准线l的方程为:x=
,两条渐近线方程为:y=±
x.
∴两交点坐标为 P(
,
)、Q(
,-
).
设M为PQ与x轴的交点
∵△PFQ为等边三角形,则有|MF|=
|PQ|(如图).
∴c-
=
•(
+
),即
=
.
解得 b=
a,c=2a.
∴e=
=2.
(2)由(1)得双曲线C的方程为
-
=1.直线方程为y=ax+
a
把y=ax+
a代入得(a2-3)x2+2
a2x+6a2=0.
依题意
∴a2<6,且a2≠3.
设P(x1,y1),Q(x2,y2),
∴x1+x2=
,x1x2=
∴双曲线C被直线y=ax+b截得的弦长为l=
=
=
=
∵l=
=12a.
∴144a2=(1+a2)•
.
整理得 13a4-77a2+102=0.
∴a2=2或a2=
.
∴双曲线C的方程为:
-
=1或
-
=1.
 解:(1)双曲线C的右准线l的方程为:x=
解:(1)双曲线C的右准线l的方程为:x=| a2 |
| c |
| b |
| a |
∴两交点坐标为 P(
| a2 |
| c |
| ab |
| c |
| a2 |
| c |
| ab |
| c |
设M为PQ与x轴的交点
∵△PFQ为等边三角形,则有|MF|=
| ||
| 2 |
∴c-
| a2 |
| c |
| ||
| 2 |
| ab |
| c |
| ab |
| c |
| c2-a2 |
| c |
| ||
| c |
解得 b=
| 3 |
∴e=
| c |
| a |
(2)由(1)得双曲线C的方程为
| x2 |
| a2 |
| y2 |
| 3a2 |
| 3 |
把y=ax+
| 3 |
| 3 |
依题意
|
∴a2<6,且a2≠3.
设P(x1,y1),Q(x2,y2),
∴x1+x2=
2
| ||
| 3-a2 |
| 6a2 |
| a2-3 |
∴双曲线C被直线y=ax+b截得的弦长为l=
| (x1-x2)2+(y1-y2)2 |
| (1+a2)(x1-x2)2 |
| (1+a2)[(x1+x2)2-4x1x2] |
(1+a2)
|
∵l=
| b2e2 |
| a |
∴144a2=(1+a2)•
| 72a2-12a4 |
| (a2-3)2 |
整理得 13a4-77a2+102=0.
∴a2=2或a2=
| 51 |
| 13 |
∴双曲线C的方程为:
| x2 |
| 2 |
| y2 |
| 6 |
| 13x2 |
| 51 |
| 13y2 |
| 153 |
点评:本题以双曲线的性质为载体,考查双曲线的标准方程,考查双曲线的离心率,考查直线与双曲线的位置关系,解题的关键是利用韦达定理求弦长

练习册系列答案
相关题目