题目内容
对于无穷数列![]() 和函数
和函数![]() ,若
,若![]() ,则称
,则称![]() 是数列
是数列![]() 的母函数.
的母函数.
(Ⅰ)定义在![]() 上的函数
上的函数![]() 满足:对任意
满足:对任意![]() ,都有
,都有![]() ,且
,且![]() ;又数列
;又数列![]() 满足:
满足:![]() .
.
(1) 求证:![]() 是数列
是数列![]() 的母函数;
的母函数;
(2)求数列![]() 的前项
的前项![]() 和
和![]() .
.
(Ⅱ)已知![]() 是数列
是数列![]() 的母函数,且
的母函数,且![]() .若数列
.若数列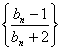 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
解:(Ⅰ)(1)由题知![]() ,且
,且
![]()
![]()
![]() .
.
![]()
![]() 是数列
是数列![]() 的母函数;
的母函数;
(2) 由(1) 知:![]() 是首项和公差均为
是首项和公差均为![]() 的等差数列,故
的等差数列,故![]() .
.
![]() ①
①
![]() ②
②
①-②得:
![]() .
.
![]() .
.
(Ⅱ)由题知:![]() ,
,![]() .
.
![]()
![]() .
.
从而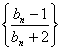 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
 .
.
又![]()
故当![]() 时,有:
时,有:
![]()
![]()
![]()
![]() .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 和函数
和函数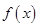 ,若
,若 ,则称
,则称 上的函数
上的函数 满足:对任意
满足:对任意 ,都有
,都有 ,且
,且 ;又数列
;又数列 满足:
满足: .
.  是数列
是数列 的母函数;
的母函数; 和
和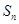 .
. 是数列
是数列 的母函数,且
的母函数,且 .若数列
.若数列 的前
的前 ,求证:
,求证: .
.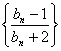 的前
的前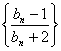 的前
的前