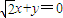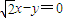题目内容
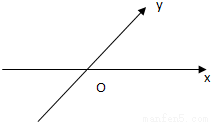
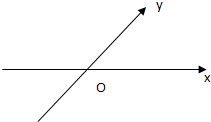 如图,在平面斜坐标中∠xoy=45°,斜坐标定义为
如图,在平面斜坐标中∠xoy=45°,斜坐标定义为| OP |
| e1 |
| e2 |
| e1 |
| e2 |
| MF |
| MF |
分析:欲求点M在斜坐标系中的轨迹方程,设P(x,y),只须求出其坐标x,y之间的关系即可,根据 |
|=|
|建立等式关系,解之即可求出点M的轨迹方程.
| AP |
| BP |
解答:解:设M(x,y),∵F1(-1,0),F2(1,0),
∴由定义知,
=-[(x+1)
+y
],
=-[(x-1)
+y
],
由 |
1|=|
2|得:
|(x +1)
+y
|=|(x -1)
+y
|,
∴
=
,
整理得:
x+y=0.
故选C.
∴由定义知,
| MF 1 |
| e1 |
| e2 |
| MF 2 |
| e1 |
| e2 |
由 |
| MF |
| MF |
|(x +1)
| e1 |
| e2 |
| e1 |
| e2 |
∴
(x+1)2+y2+2(x+1)y×
|
(x-1)2+y2+2(x-1)y×
|
整理得:
| 2 |
故选C.
点评:本题是新信息题,读懂信息,斜坐标系是一个两坐标轴夹角为45°的坐标系,这是区别于以前学习过的坐标系的地方,本小题主要考查向量的模、平面向量的基本定理及其意义、轨迹方程等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
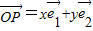 (其中
(其中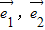 分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足
分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足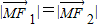 ,则点M在斜坐标系中的轨迹方程( )
,则点M在斜坐标系中的轨迹方程( )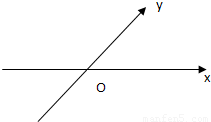
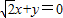
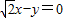
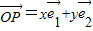 (其中
(其中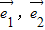 分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足
分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足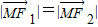 ,则点M在斜坐标系中的轨迹方程( )
,则点M在斜坐标系中的轨迹方程( )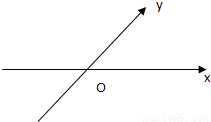
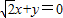
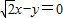
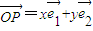 (其中
(其中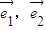 分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足
分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足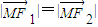 ,则点M在斜坐标系中的轨迹方程( )
,则点M在斜坐标系中的轨迹方程( )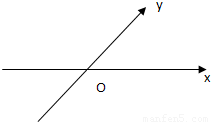
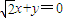
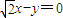
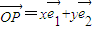 (其中
(其中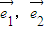 分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足
分别为斜坐标系的x轴,y轴的单位向量),则点P的坐标为(x,y).若F1(-1,0),F2(1,0),且动点M(x,y)满足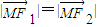 ,则点M在斜坐标系中的轨迹方程( )
,则点M在斜坐标系中的轨迹方程( )