题目内容
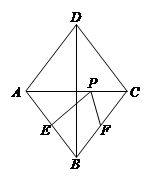
如图所示,在菱形ABCD中,对角线AC=6,BD=8,点E、F分别是边AB、BC的中点,点P在AC上运动,在运动过程中,存在PE+PF的最小值,则这个最小值是( )
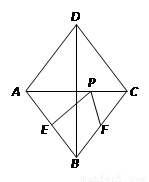
A.3 B.4 C.5 D.6
【答案】
C
【解析】解:AC交BD于O,
作E关于AC的对称点N,连接NF,交AC于P,则此时EP+FP的值最小,
∴PN=PE,
∵四边形ABCD是菱形,
∴∠DAB=∠BCD,AD=AB=BC=CD,OA=OC,OB=OD,AD∥BC,
∵E为AB的中点,
∴N在AD上,且N为AD的中点,
NF过O点,
即P、O重合,
∵AN∥BF,AN=BF,
∴四边形ANFB是平行四边形,
∴NF=AB,
∵菱形ABCD,
∴AC⊥BD,OA=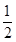 AC=3,BO=
AC=3,BO=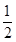 BD=4,
BD=4,
由勾股定理得:AB2= AO2+BO2 =5,
故答案为:5.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
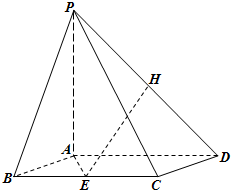 如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且AB=2,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为菱形,且AB=2,PA⊥平面ABCD,∠ABC=60°,E是BC的中点.
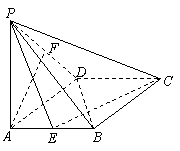 (1) 求证:PC⊥BD;
(1) 求证:PC⊥BD;