题目内容
以下四个命题:①若α是第一象限角,则sinα+cosα>1;
②存在α使sinα=
| 1 |
| 3 |
| 2 |
| 3 |
③若|cos2α|=-cos2α,则α终边在第一、二象限;
④若tan(5π+α)=-2且cosα>0,则sin(α-π)=
2
| ||
| 5 |
其中正确命题的序号是
分析:根据三角函数线判断①对,根据平方关系判断②不对,根据三角函数值的符号判断③不对,根据三角函数值的符号、诱导公式、同角三角函数的基本关系进行化简和求值,判断④对,综合可得答案.
解答:解:①、∵α是第一象限角,∴根据正弦和余弦线知,sinα+cosα>1,故①正确;
②、由sin2α+cos2α=1知,不存在角α满足条件,故②不对;
③、∵|cos2α|=-cos2α,∴cos2α<0,即
+2kπ<2α<
+2kπ,
∴
+kπ<α<
+kπ(k∈Z),故③不对;
④、∵tan(5π+α)=-2,∴tanα=-2<0,再由cosα>0知,α是第四象限角,
由同角的三角函数的基本关系求出sinα=-
,∴sin(α-π)=-sinα=
,故④正确,
故答案为:①④.
②、由sin2α+cos2α=1知,不存在角α满足条件,故②不对;
③、∵|cos2α|=-cos2α,∴cos2α<0,即
| π |
| 2 |
| 3π |
| 2 |
∴
| π |
| 4 |
| 3π |
| 4 |
④、∵tan(5π+α)=-2,∴tanα=-2<0,再由cosα>0知,α是第四象限角,
由同角的三角函数的基本关系求出sinα=-
2
| ||
| 5 |
2
| ||
| 5 |
故答案为:①④.
点评:本题是有关三角函数的综合题,考查了三角函数线的应用,三角函数值的符号的应用,同角三角函数的基本关系应用,考查了知识的综合应用.

练习册系列答案
相关题目
 ①“若对所有满足
①“若对所有满足 的
的 ,都有
,都有 ”的否命题;
”的否命题; 若直线
若直线 的方向向量为
的方向向量为 =(1,
=(1, ,2),平面
,2),平面 的法向量为
的法向量为 =(-2,0,1),
=(-2,0,1), 与曲线
与曲线 (0﹤k﹤9)有相同的焦点;
(0﹤k﹤9)有相同的焦点; 是空间四点,若
是空间四点,若 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么 =
=
 +
+
 +
+
 ,则点M与点A、B、C共面;
,则点M与点A、B、C共面; -
-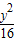 =1的两焦点为F1、F2,点P为双曲线上一点,且
=1的两焦点为F1、F2,点P为双曲线上一点,且 •
• =0,则△PF1F2的面积为16;
=0,则△PF1F2的面积为16; +
+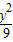 =1与曲线
=1与曲线 +
+ =1(0<k<9)有相同的焦点;
=1(0<k<9)有相同的焦点; ①“若对所有满足
①“若对所有满足 的
的 ,都有
,都有 ”的否命题;
”的否命题; 的方向向量为
的方向向量为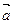 =(1,
=(1, ,2),平面
,2),平面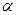 的法向量为
的法向量为 =(-2,0,1),
=(-2,0,1),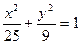 与曲线
与曲线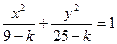 (0﹤k﹤9)有相同的焦点;
(0﹤k﹤9)有相同的焦点; 是空间四点,若
是空间四点,若 不能构成空间的一个基底,那么
不能构成空间的一个基底,那么