题目内容
15.已知数列{bn}满足3(n+1)bn=nbn+1,且b1=3.(1)求数列{bn}的通项公式;
(2)已知$\frac{{a}_{n}}{{b}_{n}}$=$\frac{n+1}{2n+3}$,求证:$\frac{5}{6}$≤$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<1$\end{array}$.
分析 (1)由于$\frac{{b}_{n+1}}{n+1}=3\frac{{b}_{n}}{n}$,令${c}_{n}=\frac{{b}_{n}}{n}$,则{cn}是等比数列,故bn=n3n;
(2)由$\frac{{a}_{n}}{{b}_{n}}$=$\frac{n+1}{2n+3}$,可知an=$\frac{n+1}{2n+3}{b}_{n}$,将$\frac{1}{{a}_{n}}$=$\frac{1}{n×{3}^{n-1}}$-$\frac{1}{(n+1)×{3}^{n}}$放大至$\frac{1}{(n-1)×{3}^{n-1}}$-$\frac{1}{n×{3}^{n}}$ (n>1),$\frac{1}{{a}_{1}}$放大至1-$\frac{1}{3}$,相加即可$\end{array}$.
解答 (1)解:∵3(n+1)bn=nbn+1,
∴$\frac{{b}_{n+1}}{n+1}=3\frac{{b}_{n}}{n}$,
令${c}_{n}=\frac{{b}_{n}}{n}$,则c1=$\frac{{b}_{1}}{1}$=3,$\frac{{c}_{n+1}}{{c}_{n}}$=3,
所以{cn}是以首项为3,公比也为3的等比数列,
从而cn=3n,
故bn=ncn=n3n;
(2)证明:由(1)及$\frac{{a}_{n}}{{b}_{n}}$=$\frac{n+1}{2n+3}$,可知an=$\frac{n+1}{2n+3}{b}_{n}$,
所以$\frac{n+1}{2n+3}{b}_{n}$=$\frac{n(n+1)}{2n+3}×{3}^{n}$,
则$\frac{1}{{a}_{n}}$=$\frac{1}{{3}^{n}}×\frac{2n+3}{n(n+1)}$
=$\frac{1}{n×{3}^{n-1}}$-$\frac{1}{(n+1)×{3}^{n}}$
<$\frac{1}{(n-1)×{3}^{n-1}}$-$\frac{1}{n×{3}^{n}}$,
显然$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$≥$\frac{1}{{a}_{1}}$=$\frac{2+3}{3×2}$=$\frac{5}{6}$;
另一方面$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<$\frac{1}{{a}_{1}}$+($\frac{1}{3}-\frac{1}{2×{3}^{2}}$)+…+($\frac{1}{(n-1)×{3}^{n-1}}$-$\frac{1}{n×{3}^{n}}$)
<1-$\frac{1}{3}$+($\frac{1}{3}-\frac{1}{2×{3}^{2}}$)+…+($\frac{1}{(n-1)×{3}^{n-1}}$-$\frac{1}{n×{3}^{n}}$)
=1-$\frac{1}{n×{3}^{n}}$<1$\end{array}$.
综上,$\frac{5}{6}$≤$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+…+$\frac{1}{{a}_{n}}$<1$\end{array}$.
点评 本题考查了递推式的应用、“裂项求和”以及放缩法,考查了推理能力与计算能力,属于难题.

| A. | (-∞,-$\sqrt{2}$)∪[$\sqrt{2}$,+∞) | B. | [-2,2] | C. | [-2,-$\sqrt{2}$]∪[$\sqrt{2}$,2] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
 的导函数
的导函数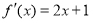 ,则数列
,则数列
 的前
的前 项和是( )
项和是( ) B.
B.
 D.
D.
 铁皮剪出一个圆心角为α的扇形,制成一个圆锥形容器,扇形的圆心角α多大时,容器的容积最大?
铁皮剪出一个圆心角为α的扇形,制成一个圆锥形容器,扇形的圆心角α多大时,容器的容积最大?