题目内容
设关于 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式
 的解集为
的解集为 .
.
(Ⅰ)当 时,求集合
时,求集合 ;(Ⅱ)若
;(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围.
 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式 的解集为
的解集为 .
.(Ⅰ)当
 时,求集合
时,求集合 ;(Ⅱ)若
;(Ⅱ)若 ,求实数
,求实数 的取值范围.
的取值范围. (Ⅰ) (Ⅱ)
(Ⅱ)
 (Ⅱ)
(Ⅱ)
本试题主要是考查了结合的运算,以及不等式的求解的综合运用。
(1)当a=1时,可知x的不等式的解集,然后得到集合M
(2)由已知可知集合N,然后根据集合间的包含关系可知道,参数a的范围。
解:(Ⅰ)当 时, 由已知得
时, 由已知得 . 解得
. 解得 .
.
所以 . ……4分
. ……4分
(Ⅱ) 由已知得 . ……6分
. ……6分
①当 时, 因为
时, 因为 ,所以
,所以 .
.
因为 ,所以
,所以 ,解得
,解得
②若 时,
时,  ,显然有
,显然有 ,所以
,所以 成立
成立
③若 时, 因为
时, 因为 ,所以
,所以 . ……9分
. ……9分
又 ,因为
,因为 ,所以
,所以 ,解得
,解得 …11分
…11分
综上所述, 的取值范围是
的取值范围是 . …12分
. …12分
(1)当a=1时,可知x的不等式的解集,然后得到集合M
(2)由已知可知集合N,然后根据集合间的包含关系可知道,参数a的范围。
解:(Ⅰ)当
 时, 由已知得
时, 由已知得 . 解得
. 解得 .
. 所以
 . ……4分
. ……4分(Ⅱ) 由已知得
 . ……6分
. ……6分①当
 时, 因为
时, 因为 ,所以
,所以 .
.因为
 ,所以
,所以 ,解得
,解得
②若
 时,
时,  ,显然有
,显然有 ,所以
,所以 成立
成立 ③若
 时, 因为
时, 因为 ,所以
,所以 . ……9分
. ……9分又
 ,因为
,因为 ,所以
,所以 ,解得
,解得 …11分
…11分综上所述,
 的取值范围是
的取值范围是 . …12分
. …12分
练习册系列答案
相关题目
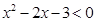 的解集为A,不等式
的解集为A,不等式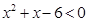 的解集为B.求A∩B;
的解集为B.求A∩B; 
 B.
B.


 ,集合
,集合  ,
, ,则
,则  ( )
( )



 ,
, 则
则 =( )
=( )

 }
}
 ,
, 为集合
为集合 的非空真子集,且
的非空真子集,且 不相等,若
不相等,若 ,则
,则 ( ).
( ).
 ,集合
,集合 ,则
,则 ( )
( )



 ,若
,若 ,则
,则 .
.  ,则
,则 等于 ( )
等于 ( )


