题目内容
由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形的面积的最小值是分析:由图形将阴影部分的面积用定积分表示出来,再利用定积分的运算规则将面积表示为t的函数,进行判断得出面积的最小值
解答: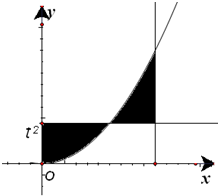 解:由题意及图象,曲线y=x2和直线y=t2交点坐标是(t,t2)
解:由题意及图象,曲线y=x2和直线y=t2交点坐标是(t,t2)
故阴影部分的面积是∫0t(t2-x2)dx+∫t1(-t2+x2)dx=(t2x-
x3)|0t+(-t2x+
x3)|t1=
t3-t2+
令p=
t3-t2+
,则p′=4t2-2t=2t(2t-1),知p=
t3-t2+
在(0,1)先减后增,在t=
时取到最小值,
故面积的最小值是
×(
)3-(
)2+
=
故答案为:
.
 解:由题意及图象,曲线y=x2和直线y=t2交点坐标是(t,t2)
解:由题意及图象,曲线y=x2和直线y=t2交点坐标是(t,t2)故阴影部分的面积是∫0t(t2-x2)dx+∫t1(-t2+x2)dx=(t2x-
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
令p=
| 4 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
故面积的最小值是
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
故答案为:
| 1 |
| 4 |
点评:本题考查求定积分,解题的关键是根据图象与函数解析式将面积用积分表示出来,利用积分的定义得到关于变量t的表达式,再研究其单调性求出最值,本题运算量较大涉及到的考点较多,综合性强,运算量大,极易因运算、变形出错.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )
由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
 由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )
由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( ) 由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是多少?
由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是多少?