题目内容
在△ABC中，其三边分别为a、b、c，且三角形的面积S=
，则角C=（ ）
| a2+b2-c2 |
| 4 |
| A．45° | B．150° | C．30° | D．135° |
由三角形的面积公式得：S=
absinC，而S=
(a2+b2-c2)，
所以
absinC=
(a2+b2-c2)，即sinC=
=cosC，
则sinC=cosC，即tanC=1，又∠C∈（0，180°），
则∠C=45°．
故选A
| 1 |
| 2 |
| 1 |
| 4 |
所以
| 1 |
| 2 |
| 1 |
| 4 |
| a2+b2-c2 |
| 2ab |
则sinC=cosC，即tanC=1，又∠C∈（0，180°），
则∠C=45°．
故选A
练习册系列答案
相关题目
在△ABC中，其三边分别为a、b、c，且三角形的面积S=
，则角C=（ ）
| a2+b2-c2 |
| 4 |
| A、45° | B、150° |
| C、30° | D、135° |
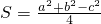，则角C=
，则角C=（ ）