题目内容
函数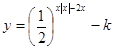 的零点有三个,则实数k的取值范围是( )
的零点有三个,则实数k的取值范围是( )
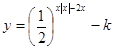 的零点有三个,则实数k的取值范围是( )
的零点有三个,则实数k的取值范围是( )A.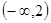 | B.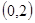 | C.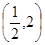 | D.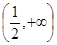 |
C
令t=x|x|-2x,问题转化为函数y=x|x|-2x-t有三个零点;又设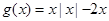
G(x是奇函数;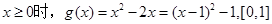 上是减函数,
上是减函数,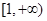 上是增函数;并且,
上是增函数;并且,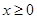 时,g(x)最小是-1;则x<0是g(x)最大是1.所以g(x)在
时,g(x)最小是-1;则x<0是g(x)最大是1.所以g(x)在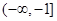 上是增函数,在[-1,1]上是减函数;在
上是增函数,在[-1,1]上是减函数;在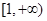 上是增函数;所以要使函数y=x|x|-2x-t有三个零点
上是增函数;所以要使函数y=x|x|-2x-t有三个零点
需使-1<t<1.故实数k应满足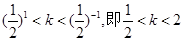 。故选C
。故选C
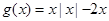
G(x是奇函数;
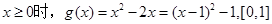 上是减函数,
上是减函数,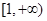 上是增函数;并且,
上是增函数;并且,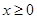 时,g(x)最小是-1;则x<0是g(x)最大是1.所以g(x)在
时,g(x)最小是-1;则x<0是g(x)最大是1.所以g(x)在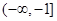 上是增函数,在[-1,1]上是减函数;在
上是增函数,在[-1,1]上是减函数;在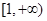 上是增函数;所以要使函数y=x|x|-2x-t有三个零点
上是增函数;所以要使函数y=x|x|-2x-t有三个零点需使-1<t<1.故实数k应满足
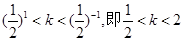 。故选C
。故选C
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
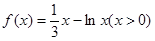 ,则
,则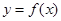 ( )
( )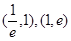 内均有零点
内均有零点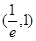 内有零点,在区间
内有零点,在区间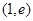 内无零点
内无零点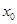 是方程8-x=lgx的解,且
是方程8-x=lgx的解,且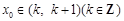 ,则k= .
,则k= . 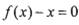 有实数根;
有实数根;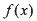 的导数
的导数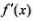 (满足
(满足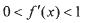 ”
”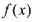 为集合M中的任一元素,试证明万程
为集合M中的任一元素,试证明万程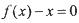 只有一个实根;
只有一个实根;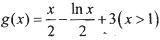 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;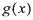 定义域内的任一区间
定义域内的任一区间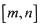 ,都存在
,都存在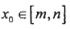 ,使得
,使得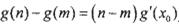 ”,请利用函数
”,请利用函数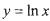 的图象说明这一结论.
的图象说明这一结论. 在
在 内有解,则
内有解,则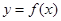 的图象是
的图象是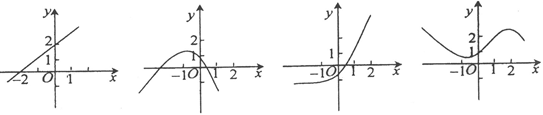
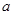 是实数,若函数
是实数,若函数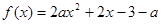 在区间
在区间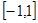 上恰好有一个零点,则
上恰好有一个零点,则 ; ②
; ② ; ③设
; ③设 、
、 是方程
是方程 的两个实根,且
的两个实根,且 ,则关于
,则关于 的不等式
的不等式 的
的 ; ④已知实数
; ④已知实数 满足
满足 (
( ),则
),则 的
的 。其中正确命题的序号为 (把你认为正确的命题的序号都填上)
。其中正确命题的序号为 (把你认为正确的命题的序号都填上)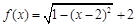 ,对任意x1,x2,且
,对任意x1,x2,且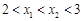 ,那么有( )
,那么有( )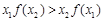

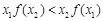
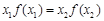
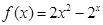 ,
, 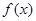 的零点在那个区间( )
的零点在那个区间( )