题目内容
(本小题满分12分) 已知函数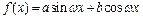 (
( R,且
R,且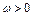 )的部分图象如图所示.
)的部分图象如图所示.
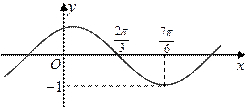
(1) 求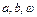 的值;
的值;
(2) 若方程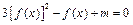
在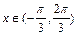 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围.
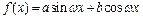 (
( R,且
R,且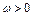 )的部分图象如图所示.
)的部分图象如图所示.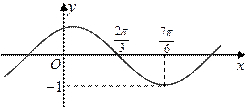
(1) 求
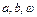 的值;
的值;(2) 若方程
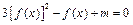
在
 内有两个不同的解,求实数m的取值范围.
内有两个不同的解,求实数m的取值范围.(1)  ,
, (2) m的取值范围是:
(2) m的取值范围是: 或
或
 ,
, (2) m的取值范围是:
(2) m的取值范围是: 或
或
(1) 由图象易知函数 的周期为
的周期为 (
(

 )=
)= ,∴
,∴ .
.
又, 且
且 , 即
, 即 , 解得:
, 解得:  . 所以,
. 所以,

 . [也可以按以下解释: 上述函数的图象可由
. [也可以按以下解释: 上述函数的图象可由 的图象沿
的图象沿 轴负方向平移
轴负方向平移 个单位而得到,∴其解析式为
个单位而得到,∴其解析式为 .∴
.∴
(2) ∴
∴ ,∴
,∴ .设
.设 ,
,
问题等价于方程 在(0,1)仅有一根或有两个相等的根.
在(0,1)仅有一根或有两个相等的根.
方法一:∵-m = 3t2 -t,t Î(0, 1). 作出曲线C:y = 3t2 -t,t Î(0, 1)与直线l:y = -m的图象.
∵t = 时,y =
时,y = ;t = 0时,y = 0;t = 1时,y = 2.
;t = 0时,y = 0;t = 1时,y = 2.
∴当 -m = 或0≤-m<2时,直线l与曲线C有且只有一个公共点.
或0≤-m<2时,直线l与曲线C有且只有一个公共点.
∴m的取值范围是: 或
或
方法二:当 仅有一根在(0, 1)时,令
仅有一根在(0, 1)时,令 则
则 得到
得到 ; 或
; 或 时
时 ,或
,或 时
时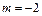 (舍去)
(舍去)
当两个等根同在(0,1)内时得到 ,
,
综上所述,m的取值范围是: 或
或
 的周期为
的周期为 (
(

 )=
)= ,∴
,∴ .
.又,
 且
且 , 即
, 即 , 解得:
, 解得:  . 所以,
. 所以,
 . [也可以按以下解释: 上述函数的图象可由
. [也可以按以下解释: 上述函数的图象可由 的图象沿
的图象沿 轴负方向平移
轴负方向平移 个单位而得到,∴其解析式为
个单位而得到,∴其解析式为 .∴
.∴
(2)
 ∴
∴ ,∴
,∴ .设
.设 ,
,问题等价于方程
 在(0,1)仅有一根或有两个相等的根.
在(0,1)仅有一根或有两个相等的根. 方法一:∵-m = 3t2 -t,t Î(0, 1). 作出曲线C:y = 3t2 -t,t Î(0, 1)与直线l:y = -m的图象.
∵t =
 时,y =
时,y = ;t = 0时,y = 0;t = 1时,y = 2.
;t = 0时,y = 0;t = 1时,y = 2. ∴当 -m =
 或0≤-m<2时,直线l与曲线C有且只有一个公共点.
或0≤-m<2时,直线l与曲线C有且只有一个公共点.∴m的取值范围是:
 或
或
方法二:当
 仅有一根在(0, 1)时,令
仅有一根在(0, 1)时,令 则
则 得到
得到 ; 或
; 或 时
时 ,或
,或 时
时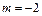 (舍去)
(舍去) 当两个等根同在(0,1)内时得到
 ,
,
综上所述,m的取值范围是:
 或
或

练习册系列答案
相关题目
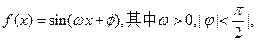
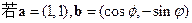 ,且
,且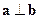 ,又知函数
,又知函数 (1)求
(1)求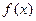 的解析式;
的解析式;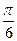 个单位得到
个单位得到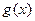 的图象,求
的图象,求 )在区间
)在区间 的图像如下:那么
的图像如下:那么 =( )
=( )
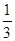


 在一个最小正周期长的区间上的图像与函数
在一个最小正周期长的区间上的图像与函数 的图像所围成的封闭图形的面积是________________。
的图像所围成的封闭图形的面积是________________。 图象上的一个最高点为
图象上的一个最高点为 ,由这个最高点到相邻最低点间的曲线与
,由这个最高点到相邻最低点间的曲线与 轴相交于
轴相交于 ,并写出这个函数的单调区间.
,并写出这个函数的单调区间.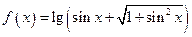 的奇偶性.
的奇偶性. 的图象( ).
的图象( ). 轴对称
轴对称 轴对称
轴对称 对称
对称 ,⑴求
,⑴求 的值;⑵求
的值;⑵求 的值.
的值.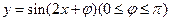 是
是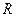 上的偶函数,则
上的偶函数,则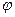 的值是( )
的值是( )