题目内容
某市高三数学抽样考试中，对90分以上(含90分)的成绩进行统计，其频率分布图如图所示，已知130～140分数段的人数为90，90～100分数段的人数为a，则下图所示程序框图的运算结果为(注：n！＝1×2×3×…×n，如5！＝1×2×3×4×5)( )
| A．800! | B．810! | C．811! | D．812! |
B
解析试题分析：设样本容量为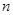
，130～140分数段的频率为0.05，则0.05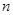=90，解得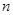=1800，即样本容量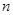=1800， 90～100分数段的频率为0.45，故90～100分数段的人数为
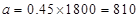，根据程序框图可知是计算
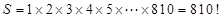，故答案选Ｂ．
考点：频率分布直方图，算法框图．
巧学巧练系列答案某研究型学习课程的学生中，高一年级有30名，高二年级有40名．现用分层抽样的方法在这70名学生中抽取一个样本，已知在高一年级的学生中抽取了6名，则在高二年级的学生中应抽取的人数为( )
| A．6 | B．8 | C．10 | D．12 |
一组数据的方差是s2，将这组数据中的每一个数据都乘以2，所得到的一组数据的方差是
| A．2s2 | B．4s2 | C．8s2 | D．16s2 |
对具有线性相关关系的变量
，
测得一组数据如下表：
| x | 2 | 4 | 5 | 6 | 8 |
| y | 20 | 40 | 60 | 80 | 100 |
.据此模型预测
时，的估计值为（ ）A. 320 B. 320.5 C. 322.5 D. 321.5
某车间生产一种玩具,为了要确定加工玩具所需要的时间,进行了10次实验,数据如下:
| 玩具个数 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 加工时间 | 4 | 7 | 12 | 15 | 21 | 25 | 27 | 31 | 37 | 41 |
，则它的截距是 ( )A.
＝11－22； B.＝11－22； C.＝22－11； D.＝22－11. 为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，在下面的抽样方法中，最合理的抽样方法是( )
| A．简单随机抽样 | B．按性别分层抽样 |
| C．按学段分层抽样 | D．系统抽样 |
某地区教育主管部门为了对该地区模拟考试成绩进行分析，抽取了总成绩介于350分到650分之间的10 000名学生成绩，并根据这10 000名学生的总成绩画了样本的频率分布直方图(如图所示)，则总成绩在[400,500)内共有( )．
| A．5000人 | B．4500人 | C．3250人 | D．2500人 |
某班的全体学生参加英语测试，成绩的频率分布直方图如图，数据的分组依次为：[20,40)，[40,60)，[60,80)，[80,100]．若低于60分的人数是15，则该班的学生人数是( )．
| A．45 | B．50 | C．55 | D．60 |
为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样的方法从该地区调查了500位老年人，结果如下表：
| | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
K2＝
A．估计该地区老年人中，需要志愿者提供帮助的老年人的比例为10%
B．估计该地区老年人中，需要志愿者提供帮助的老年人的比例为20%
C．有99%的把握认为该地区的老年人需要志愿者提供帮助与性别有关
D．有99%的把握认为该地区的老年人需要志愿者提供帮助与性别无关