题目内容
已知点F为双曲线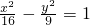 右焦点,M是双曲线右支上的一动点,A(5,4),则4MF-5MA的最大值为________.
右焦点,M是双曲线右支上的一动点,A(5,4),则4MF-5MA的最大值为________.
9
分析:由双曲线的定义可得 4MF-5MA=4•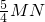 -5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,
-5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,
最大值为 5AN=5(5- ).
).
解答:点F(5,0),离心率e= ,设M到右准线的距离等于MN,则由双曲线的定义可得
,设M到右准线的距离等于MN,则由双曲线的定义可得
4MF-5MA=4•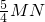 -5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,
-5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,
最大值为 5AN=5(5- )=9,
)=9,
故答案为:9.
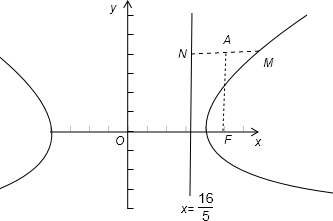
点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,判断当M,A,N 三点共线时,5(MN-MA)最大,是解题的关键.
分析:由双曲线的定义可得 4MF-5MA=4•
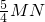 -5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,
-5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,最大值为 5AN=5(5-
 ).
).解答:点F(5,0),离心率e=
 ,设M到右准线的距离等于MN,则由双曲线的定义可得
,设M到右准线的距离等于MN,则由双曲线的定义可得4MF-5MA=4•
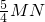 -5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,
-5 MA=5(MN-MA),故当M,A,N 三点共线时,5(MN-MA)最大,最大值为 5AN=5(5-
 )=9,
)=9,故答案为:9.

点评:本题考查双曲线的定义和标准方程,以及双曲线的简单性质的应用,判断当M,A,N 三点共线时,5(MN-MA)最大,是解题的关键.

练习册系列答案
相关题目