题目内容
设A和B是抛物线上的两个动点,且在A和B处的抛物线切线相互垂直,已知由A、B及抛物线的顶点所成的三角形重心的轨迹也是一抛物线,记为L1.对L1重复以上过程,又得一抛物线L2,余类推.设如此得到抛物线的序列为L1,L2,…,Ln,若抛物线的方程为y2=6x,经专家计算得,L1:y2=2(x-1),L2:y2=
(x-1-
)=
(x-
),L3:y2=
(x-1-
-
)=
(x-
),…,Ln:y2=
(x-
). 则2Tn-3Sn=
| 2 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 9 |
| 1 |
| 3 |
| 1 |
| 9 |
| 2 |
| 9 |
| 13 |
| 9 |
| 2 |
| Sn |
| Tn |
| Sn |
-1
-1
.分析:写出分子上的数列观察数列的结构,看出数列的前后两项之差是一个等比数列,利用叠加的方法做出第n项,同样写出分母上数列的项观察得到这是一个等比数列,写出通项,做出最后两个数的差,得到结果.
解答:解:由题意知1,4,13,40…组成一个数列,
数列的前后两项之差是一个等比数列,
即an-an-1=3n-1,
…
a3-a2=32
a2-a1=3,
把上述式子相加得到an-1=3+32+…+3n-1
∴Tn=
由1,3,9,27…组成的数列的通项是3n-1,
∴sn=3n-1
∴2Tn-3Sn=2×
-3×3n-1=-1
故答案为:-1
数列的前后两项之差是一个等比数列,
即an-an-1=3n-1,
…
a3-a2=32
a2-a1=3,
把上述式子相加得到an-1=3+32+…+3n-1
∴Tn=
| 3n-1 |
| 2 |
由1,3,9,27…组成的数列的通项是3n-1,
∴sn=3n-1
∴2Tn-3Sn=2×
| 3n-1 |
| 2 |
故答案为:-1
点评:本题考查归纳推理,是一个考查数列问题的题目,解题的关键是看清题目的中所给的数列的项,做出数列的通项,注意项与项数的对应.

练习册系列答案
相关题目
 上的两个动点,且在A和B处的抛物线切线相互垂直, 已知由A、B 及抛物线的顶点P所成的三角形重心的轨迹也是一抛物线, 记为L1.对
上的两个动点,且在A和B处的抛物线切线相互垂直, 已知由A、B 及抛物线的顶点P所成的三角形重心的轨迹也是一抛物线, 记为L1.对 重复以上过程,又得一抛物线L2,以此类推.设如此得到抛物线的序列为L1,L2,…,
Ln,若抛物线
重复以上过程,又得一抛物线L2,以此类推.设如此得到抛物线的序列为L1,L2,…,
Ln,若抛物线 ,经专家计算得,
,经专家计算得, ,
, ,
, ,
,
 .
. = .
= . 上的两个动点,且在A和B处的抛物线切线相互垂直, 已知由A、B及抛物线的顶点P所成的三角形重心的轨迹也是一抛物线, 记为L1.对
上的两个动点,且在A和B处的抛物线切线相互垂直, 已知由A、B及抛物线的顶点P所成的三角形重心的轨迹也是一抛物线, 记为L1.对 重复以上过程,又得一抛物线L2,以此类推.设如此得到抛物线的序列为L1,L2,…, Ln,若抛物线
重复以上过程,又得一抛物线L2,以此类推.设如此得到抛物线的序列为L1,L2,…, Ln,若抛物线 ,经专家计算得
,经专家计算得
 ,
, ,
, ,
, .
. = ▲
= ▲ 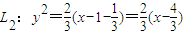 ,
,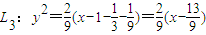 ,…,
,…,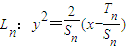 . 则2Tn-3Sn= .
. 则2Tn-3Sn= . ,
, ,…,
,…, . 则2Tn-3Sn= .
. 则2Tn-3Sn= .