题目内容
2010年5月1日上海世博会即将开幕,据悉安徽馆于4月16号建成.为更好的组织好这次盛会,来自中国科学技术大学和安徽大学的共计6名大学生志愿服务者被平均分配到安徽馆运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名中国科学技术大学志愿者的概率是
.
(1)求6名志愿者中来自中国科学技术大学和安徽大学的各几人;
(2)求清扫岗位恰好有中国科学技术大学、安徽大学的志愿者各一人的概率;
(3)设随机变量X为在维持秩序岗位服务的中国科学技术大学志愿者的人数,求X的分布列.
| 3 | 5 |
(1)求6名志愿者中来自中国科学技术大学和安徽大学的各几人;
(2)求清扫岗位恰好有中国科学技术大学、安徽大学的志愿者各一人的概率;
(3)设随机变量X为在维持秩序岗位服务的中国科学技术大学志愿者的人数,求X的分布列.
分析:(1))设中国科学技术大学有x人,则由已知可得
=1-
,解方程后可解决.
(2)因为每个岗位只能有两人,求清扫卫生岗位恰好中国科学技术大学、安徽大学各一人的概率,即中国科学技术大学、安徽大学各有一人的概率.
(3)随机变量 X的所有可能取值为:0、1、2,先求出相应的概率后,再列出分布列即可.
| 3 |
| 5 |
| ||
|
(2)因为每个岗位只能有两人,求清扫卫生岗位恰好中国科学技术大学、安徽大学各一人的概率,即中国科学技术大学、安徽大学各有一人的概率.
(3)随机变量 X的所有可能取值为:0、1、2,先求出相应的概率后,再列出分布列即可.
解答:解:(1)设中国科学技术大学有x人,则安徽大学志愿者为6-x人,由已知可得:
=1-
解得x=2,故中国科学技术大学有2人,安徽大学有4人;…(4分)
(2)P=
=
…(8分)
(3)由已知条件可得X的所有可能取值为:0、1、2
且P(X=0)=
=
;P(X=1)=
=
;P(X=2)=
=
所以X的分布列为:
| 3 |
| 5 |
| ||
|
解得x=2,故中国科学技术大学有2人,安徽大学有4人;…(4分)
(2)P=
| ||||
|
| 8 |
| 15 |
(3)由已知条件可得X的所有可能取值为:0、1、2
且P(X=0)=
| ||
|
| 2 |
| 5 |
| ||||
|
| 8 |
| 15 |
| ||
|
| 1 |
| 15 |
所以X的分布列为:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
点评:本题考查了古典概型求解,随机变量的分布列,属于常规题.遇到事件中“至多”、“至少”一类词语时常常先求出其对立事件的概率,再求出事件的概率,如(1).

练习册系列答案
相关题目
国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
| 序号( | 每天睡眠时间 (小时) | 组中值( | 频数 | 频率 ( |
| 1 | [4,5) | 4.5 | 8 | 0.04 |
| 2 | [5,6) | 5.5 | 52 | 0.26 |
| 3 | [6,7) | 6.5 | 60 | 0.30 |
| 4 | [7,8) | 7.5 | 56 | 0.28 |
| 5 | [8,9) | 8.5 | 20 | 0.10 |
| 6 | [9,10) | 9.5 | 4 | 0.02 |
 |
(Ⅰ)估计每天睡眠时间小于8小时的学生所占的百分比约是多少;
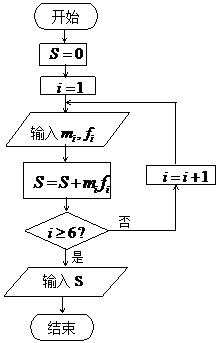
(Ⅱ)该网站利用上面的算法流程图,对样本数据作进一步统计
分析,求输出的S的值,并说明S的统计意义.
 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为 ”
”

 ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为 ”
”
 表示更换的面数,用
表示更换的面数,用 表示更换费用。
表示更换费用。