题目内容
设AB为过抛物线y2=2px（p＞0）的焦点的弦，则|AB|的最小值为（ ）
A、
| ||
| B、P | ||
| C、2P | ||
| D、无法确定 |
分析：根据抛物线方程可得焦点坐标，进而可设直线L的方程与抛物线联立根据韦达定理求得x1+x2，进而根据抛物线定义可求得|AB|的表达式，整理可得|AB|=2p（1+
），由于k=tana，进而可知当a=90°时AB|有最小值．
| 1 |
| k2 |
解答：解；焦点F坐标（
，0），设直线L过F，则直线L方程为y=k（x-
）
联立y2=2px得k2x2-（pk2+2p）x+
=0
由韦达定理得x1+x2=p+
|AB|=x1+x2+p=2p+
=2p（1+
）
因为k=tana，所以1+
=1+
=
所以|AB|=
当a=90°时，即AB垂直于X轴时，AB取得最小值，最小值是|AB|=2p
故选C
| p |
| 2 |
| p |
| 2 |
联立y2=2px得k2x2-（pk2+2p）x+
| p2k2 |
| 4 |
由韦达定理得x1+x2=p+
| 2p |
| k2 |
|AB|=x1+x2+p=2p+
| 2p |
| k2 |
| 1 |
| k2 |
因为k=tana，所以1+
| 1 |
| k2 |
| 1 |
| tan2α |
| 1 |
| sin2α |
所以|AB|=
| 2p |
| sin2α |
当a=90°时，即AB垂直于X轴时，AB取得最小值，最小值是|AB|=2p
故选C
点评：本题主要考查抛物线的应用．这道题综合了抛物线的性质、抛物线的焦点弦、直线与抛物线的关系等问题．综合性很强．
练习册系列答案
相关题目
设AB为过抛物线y2=8x的焦点的弦，则弦AB的长的最小值为（ ）
| A、2 | B、4 | C、8 | D、16 |
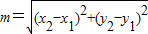，则实数m的最小值为（ ）