题目内容
在复平面中，已知点A（2，1），B（0，2），C（-2，1），O（0，0）．给出下面的结论：
①直线OC与直线BA平行；
②
+
=
；
③
+
=
；
④
=
-2
．
其中正确结论的个数是（ ）
①直线OC与直线BA平行；
②
| AB |
| BC |
| CA |
③
| OA |
| OC |
| OB |
④
| AC |
| OB |
| OA |
其中正确结论的个数是（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
分析：根据所给的复平面上的点的坐标，写出要用的向量的坐标，根据向量的加减和数乘运算，分别达到每一个式子的结果，看出四个命题中正确的个数．
解答：解：∵点A（2，1），B（0，2），C（-2，1），O（0，0）．
∴直线OC对应的向量的坐标是（-2，1）
直线BA对应的向量的坐标是（2，-1）
∵（-2）（-1）-2×1=0，
∴直线OC与直线BA平行，
故①正确，
∵
=（-2，1）
=（-2，-1）
=（4，0）
+
=（-4，0）≠
；
故②不正确，
∵
+
=（0，2）=
，
故③正确，
-2
=（0，2）-2（2，1）=（-4，0）=
，
故④正确，
综上知共有3个正确，
故选C．
∴直线OC对应的向量的坐标是（-2，1）
直线BA对应的向量的坐标是（2，-1）
∵（-2）（-1）-2×1=0，
∴直线OC与直线BA平行，
故①正确，
∵
| AB |
| BC |
| CA |
| AB |
| BC |
| CA |
故②不正确，
∵
| OA |
| OC |
| OB |
故③正确，
| OB |
| OA |
| AC |
故④正确，
综上知共有3个正确，
故选C．
点评：本题考查复平面上的点与向量的对应，是一个简单的向量加减数乘运算，解题时只要细心，就能够得到结果．
练习册系列答案
名校课堂系列答案
相关题目
③
④
．
+
=
；
+
=
；
=
+
=
；
+
=
；
=
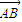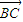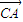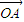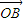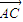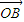-2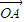
．