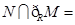题目内容

已知R是实数集，集合P={x|x2+2x-3=0}，Q={x|lnx＜1}，则P∩?RQ=（　　）
分析：通过解方程求出集合P，对数不等式的求法求出集合Q，求出Q的补集，然后求其交集．
解答：解：集合P={x|x2+2x-3=0}={1，-3}，
Q={x|lnx＜1}={x|0＜x＜e}，
所以CRQ={x|x≤0或x≥e}，
所以P∩CRQ={-3}．
故选C．
点评：本题考查集合的求法，交、并、补的基本运算，考查计算能力．
练习册系列答案
相关题目
已知R是实数集，集合M={x|
2
x
＜1，x≠0}，N={y|y=1-
t-3
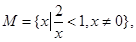
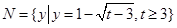，t≥3}，则N∩?RM=（　　）

已知R是实数集，集合，则

A. (－∞,2]       B. [0, 1]       C. (－∞,1]      D. [1, 2]

 
已知R是实数集，集合M={x|
2
x
＜1，x≠0}，N={y|y=1-
t-3
，t≥3}，则N∩?RM=（　　）
A．（-∞，2]B．[0，1]C．（-∞，1]D．[1，2]
已知R是实数集，集合P={x|x2+2x-3=0}，Q={x|lnx＜1}，则P∩∁RQ=（ ）
A．{-3，1}
B．{1}
C．{-3}
D．{e}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网