题目内容
若对于函数f(x)的定义域内的任一个x的值,均有f(x)=f(-x)=-f(x+
),对于下列四个函数:
①y=cos2x-cos4x;
②y=sin4x-cos4x;
③y=sin(2x+
)+cos(2x+
);
④y=|tanx|.其中符合已知条件的函数序号为
| π |
| 2 |
①y=cos2x-cos4x;
②y=sin4x-cos4x;
③y=sin(2x+
| π |
| 4 |
| π |
| 4 |
④y=|tanx|.其中符合已知条件的函数序号为
②③
②③
.分析:①函数f(x)=cos2x-cos4x,满足f(x)=f(-x),f(x+
)=f(x);
②f(x)=sin4x-cos4x=sin2x-cos2x=-cos2x,满足f(x)=f(-x),f(x+
)=-f(x);
③f(x)=sin(2x+
)+cos(2x+
)=
sin(2x+
)=-
cos2x,由②知符合条件;
④f(x)=|tanx|,满足f(x)=f(-x),f(x+
)=|cotx|≠-f(x),由此可得结论.
| π |
| 2 |
②f(x)=sin4x-cos4x=sin2x-cos2x=-cos2x,满足f(x)=f(-x),f(x+
| π |
| 2 |
③f(x)=sin(2x+
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 2 |
| 2 |
④f(x)=|tanx|,满足f(x)=f(-x),f(x+
| π |
| 2 |
解答:解:①函数f(x)=cos2x-cos4x,满足f(x)=f(-x),f(x+
)=sin2x-sin4x=sin2xcos2x,f(x)=cos2xsin2x,∴f(x+
)=f(x),故①不符合;
②f(x)=sin4x-cos4x=sin2x-cos2x=-cos2x,满足f(x)=f(-x),f(x+
)=-cos(2x+π)=cos2x=-f(x),故②符合;
③f(x)=sin(2x+
)+cos(2x+
)=
sin(2x+
)=-
cos2x,由②知符合条件;
④f(x)=|tanx|,满足f(x)=f(-x),f(x+
)=|cotx|≠-f(x),故④不符合
综上知,符合已知条件的函数序号为②③
故答案为:②③
| π |
| 2 |
| π |
| 2 |
②f(x)=sin4x-cos4x=sin2x-cos2x=-cos2x,满足f(x)=f(-x),f(x+
| π |
| 2 |
③f(x)=sin(2x+
| π |
| 4 |
| π |
| 4 |
| 2 |
| π |
| 2 |
| 2 |
④f(x)=|tanx|,满足f(x)=f(-x),f(x+
| π |
| 2 |
综上知,符合已知条件的函数序号为②③
故答案为:②③
点评:本题考查新定义,考查三角函数的化简,解题的关键是一一验证,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
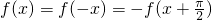 ,对于下列四个函数:
,对于下列四个函数: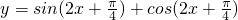 ;
;