题目内容
已知实数c≥0,曲线C:y=xN),….设点P的坐标为(a,![]() ),x1=b,0<b<a.
),x1=b,0<b<a.
(1)试用c表示a,并证明a≥1;
(2)试证明x2>x1,且xn<a(N∈N*);
(3)当c=0,b≥![]() 时,求证:
时,求证:![]()
![]() <
<![]() (k,N∈N*).
(k,N∈N*).
(1)解:点P的坐标(a,![]() )满足方程组
)满足方程组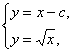 所以
所以![]() =a-c.?
=a-c.?
解a-![]() -c=0,得
-c=0,得![]() =
=![]() ,所以a=
,所以a=![]() (1+
(1+![]() ). ?
). ?
因为c≥0,所以1+![]() ≥2.所以a≥1.
≥2.所以a≥1.
(2)证明:由已知P1(b,![]() ),Q1(
),Q1(![]() +c,
+c,![]() ),P2(
),P2(![]() +c,
+c,![]() ),?
),?
即x1=b,x2=![]() +c, ?
+c, ?
x2-x1=![]() +c-b,?
+c-b,?
由(1)c=a-![]() ,所以x2-x1=
,所以x2-x1=![]() +a-
+a-![]() -b=(
-b=(![]() -
-![]() )(
)(![]() +
+![]() -1).?
-1).?
因为0<b<a,a≥1,所以x2>x1. ?
下面用数学归纳法证明xn<a(n∈N*).?
当n=1时,x1=b<a;假设当n=k时,xk<a,?
由已知,xk+1=yk+c,xk>0,所以xk+1=![]() +c=
+c=![]() +a-
+a-![]() <a.?
<a.?
综上,xn<a(n∈N*). ?
(3)解:当c=0时,![]() ≤b<a=1,xn+1=yn=
≤b<a=1,xn+1=yn=![]() (n∈N*),??
(n∈N*),??
所以xn=xn-1![]() =xn-2
=xn-2![]() =…=x1
=…=x1![]() =b
=b![]() . ?
. ?
因为b≥![]() ,所以当k≥1时,xk+2≥x3≥(
,所以当k≥1时,xk+2≥x3≥(![]() )
)![]() .?
.?
所以![]() . ?
. ?
又xk+1-xk=b![]() -b
-b![]() >0,?
>0,?
所以![]() ≤b=x1<xn<a=1,xn-x1<1-
≤b=x1<xn<a=1,xn-x1<1-![]() =
=![]() .
.
所以![]() ≤
≤![]()
![]() =
=![]() (xn+1-x1)<
(xn+1-x1)<![]() .
.


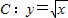 与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为
与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为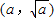 ,x1=b,0<b<a.
,x1=b,0<b<a.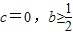 时,求证:
时,求证: .
. 与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为
与直线l:y=x-c的交点为P(异于原点O).在曲线C上取一点P1(x1,y1),过点P1作P1Q1平行于x轴,交直线l于Q1,过点Q1作Q1P2平行于y轴,交曲线C于P2(x2,y2);接着过点P2作P2Q2平行于x轴,交直线l于Q2,过点Q2作Q2P3平行于y轴,交曲线C于P3(x3,y3);如此下去,可得到点P4(x4,y4),P5(x5,y5),…,Pn(xn,yn),设点P坐标为 ,x1=b,0<b<a.
,x1=b,0<b<a. 时,求证:
时,求证: .
.