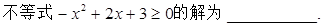题目内容
设奇函数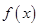 在
在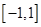 上是增函数,且
上是增函数,且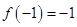 ,若函数
,若函数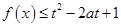 对所有的
对所有的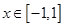 ,
,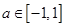 都成立,则
都成立,则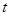 的取值范围是( )
的取值范围是( )
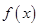 在
在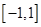 上是增函数,且
上是增函数,且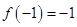 ,若函数
,若函数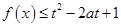 对所有的
对所有的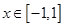 ,
,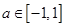 都成立,则
都成立,则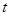 的取值范围是( )
的取值范围是( )A.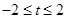 | B.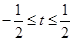 |
C.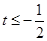 或 或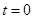 或 或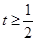 | D.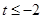 或 或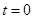 或 或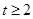 |
D
解:解:∵函数f(x)是奇函数,且在[-1,1]是单调增函数,又f(-1)=-1,
∴f(1)=1,
∴当x∈[-1,1]时,f(x)∈[-1,1]
若f(x)≤t2+2at+1对所有的x∈[-1,1]及a∈[-1,1]都成立
则t2+2at+1≥1在a∈[-1,1]上恒成立
当t=0时,不等式恒成立,满足条件;
当t>0时,不等式可化为:t2-2t+1≥1,解得t≥2;
当t<0时,不等式可化为:t2+2t+1≥1,解得t≤-2;
综上满足条件的t的范围是(-∞.-2]∪{0}∪[2,+∞)
故答案为:(-∞.-2]∪{0}∪[2,+∞)
∴f(1)=1,
∴当x∈[-1,1]时,f(x)∈[-1,1]
若f(x)≤t2+2at+1对所有的x∈[-1,1]及a∈[-1,1]都成立
则t2+2at+1≥1在a∈[-1,1]上恒成立
当t=0时,不等式恒成立,满足条件;
当t>0时,不等式可化为:t2-2t+1≥1,解得t≥2;
当t<0时,不等式可化为:t2+2t+1≥1,解得t≤-2;
综上满足条件的t的范围是(-∞.-2]∪{0}∪[2,+∞)
故答案为:(-∞.-2]∪{0}∪[2,+∞)

练习册系列答案
相关题目
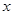 的不等式
的不等式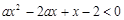
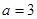 时,求此不等式解集;
时,求此不等式解集;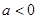 时,求此不等式解集。
时,求此不等式解集。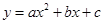 的部分对应值如下表:
的部分对应值如下表: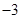
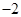
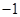
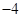
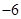
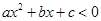 的解集为 ;
的解集为 ;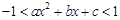 的解集为
的解集为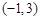 ,则实数
,则实数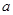 的取值范围是
的取值范围是 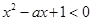 ,则实数a的取值范围是______________.
,则实数a的取值范围是______________.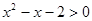 的解集为 ( )
的解集为 ( )