题目内容
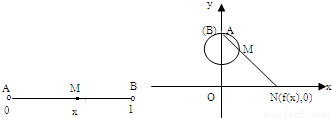
 设区间(0,1)内的实数x对应数轴上的点M(如图),将线段AB围成一个圆,使两端A、B恰好重合,再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),射线AM与ox轴交于点N(f(x),0)根据这一映射法则可得f(x)与x的函数关系式为
设区间(0,1)内的实数x对应数轴上的点M(如图),将线段AB围成一个圆,使两端A、B恰好重合,再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),射线AM与ox轴交于点N(f(x),0)根据这一映射法则可得f(x)与x的函数关系式为f(x)=
,x∈(0,1)
| cosπx |
| sinπx |
f(x)=
,x∈(0,1)
.| cosπx |
| sinπx |
分析:设AB围成圆P,圆P与y轴另一个交点为C,连接CM.利用Rt△CMA∽Rt△∠NOA,得
=
…①.圆P中利用弧度制定义和直角三角形三角函数的定义,算出AM、CM关于x的表达式,结合ON=f(x),OA=1,代入①化简,即得f(x)与x的函数关系式.
| CM |
| NO |
| AM |
| AO |
解答:解:设AB围成的圆为圆P,圆P与y轴另一个交点为C,连接CM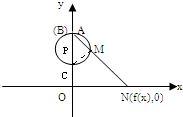
∵AC是圆N的直径
∴∠CMA=∠NOA=90°
∵∠CAM=∠NAO,
∴△CMA∽△∠NOA,得
=
…①
∵Rt△ACM中,直径AC=
,2∠ACM=
=2πx
∴AM=ACsin∠ACM=
sinπx,CM=
cosπx,
而ON=f(x),OA=1,代入①得;
=
∴f(x)与x的函数关系式为f(x)=
,x∈(0,1)
故答案为:f(x)=
,x∈(0,1)

∵AC是圆N的直径
∴∠CMA=∠NOA=90°
∵∠CAM=∠NAO,
∴△CMA∽△∠NOA,得
| CM |
| NO |
| AM |
| AO |
∵Rt△ACM中,直径AC=
| 1 |
| π |
| 弧AM | ||
|
∴AM=ACsin∠ACM=
| 1 |
| π |
| 1 |
| π |
而ON=f(x),OA=1,代入①得;
| ||
| f(x) |
| ||
| 1 |
∴f(x)与x的函数关系式为f(x)=
| cosπx |
| sinπx |
故答案为:f(x)=
| cosπx |
| sinπx |
点评:本题给出长度为1的线段围成圆后放入坐标系中,求圆的弦所在直线与x轴交点坐标的表达式,着重考查了弧度制定义、三角函数的定义和三角形相似等知识,属于基础题.

练习册系列答案
相关题目
 (2010•黄冈模拟)若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S.
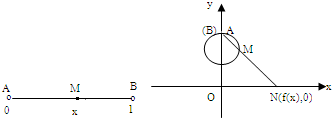
(2010•黄冈模拟)若关于x的实系数方程x2+ax+b=0有两个根,一个根在区间(0,1)内,另一根在区间(1,3)内,记点(a,b)对应的区域为S. 设区间(0,1)内的实数x对应数轴上的点M(如图),将线段AB围成一个圆,使两端A、B恰好重合,再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),射线AM与ox轴交于点N(f(x),0)根据这一映射法则可得f(x)与x的函数关系式为________.
设区间(0,1)内的实数x对应数轴上的点M(如图),将线段AB围成一个圆,使两端A、B恰好重合,再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),射线AM与ox轴交于点N(f(x),0)根据这一映射法则可得f(x)与x的函数关系式为________.