题目内容
在球面上有四点
P、A、B、C,如果PA、PB、PC两两垂直且PA=PB=PC=a.求这个球的表面积和体积.
答案:略
解析:
解析:
|
求表面积及体积主要是求半径.
解法 1:如图,设过A、B、C点的球的截面半径为r,球心到截面距离为d,球半径为R,则 ,在三棱锥P-ABC中,∵PA⊥PB,PA⊥PC,PB⊥PC,∴P在△ABC上的射影 ,在三棱锥P-ABC中,∵PA⊥PB,PA⊥PC,PB⊥PC,∴P在△ABC上的射影 是△ABC的垂心. 是△ABC的垂心.
又 PA=PB=PC,∴ 又是△ABC的外心,因此可知△ABC是等边三角形,边长为 又是△ABC的外心,因此可知△ABC是等边三角形,边长为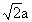 . .
∴  . .
又∵  , ,
∴  , ,
∴  . .
于是,  , ,
解 2:(补形法)因为PA、PB、PC两两垂直,所以以PA、PB、PC为基础构造一个长方体.则长方体的对角线恰为球的直径.∴ 
∴  . .
则  , ,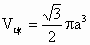 . . |

练习册系列答案
相关题目

